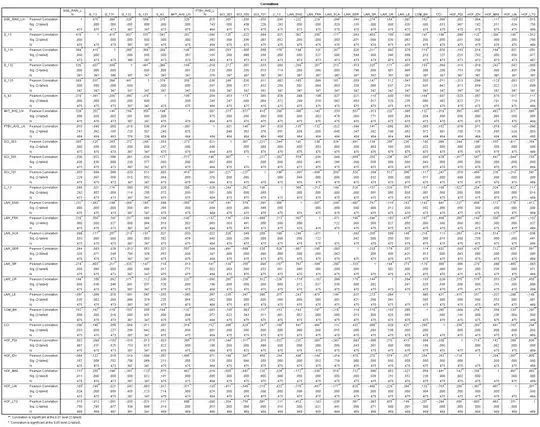
Please see the model below (link to bigger image). The independent variables are properties of 2500 companies from 32 countries, trying to explain companies' CSR (corporate social responsibility) score.
I am worried about the VIF scores of especially the LAW_, GCI_ and HOF_ variables but I really need them all included in the model to connect it to the theoretical background the model is built upon. All variables are discrete numeric values, except the law LAW_ variables: they are dummies as to which legal system applies in the companies' country of origin (either english, french, german or scandinavian).

Amongst other articles, I have read this article about dealing with collinearity. Often-suggested tips are removing the variable with highest VIF-score (in my model this would be LAW_ENG). But then other VIF-scores increase as a result. I do not have the proper knowledge to see through what is going on here and how I can solve this problem.
I have uploaded the corresponding data here (in SPSS .sav format). I would really appreciate somebody with more experience having a quick look and tell me a way to solve the collinearity problem without taking out (any or too many) variables.
Any help is greatly appreciated.
P.S. For reference, I am including a correlation table (link to bigger image):