NOTE: I'm aware that another post covers this from a slightly different angle. But the derivation (of the variance of the weighted mean) in that post does not look the one I give below, and (more importantly) there's a specific step in the derivation below that I'm confused about. My post below asks about that specific step.
I'm struggling to understand the derivation of the formula for the variance of the weighted mean effect (estimate).
I'm aware that typical meta-analysis "weights" each study by the inverse of the variance of that study's effect estimate. You then calculate a weighted mean overall/summary/meta-analytic effect by multiplying each study's effect size estimate by the relevant weight and then dividing the result by the sum of the weights.
The textbooks then tell you that the variance of the resulting weighted mean effect (estimate) is equal to the reciprocal of the sum of the weights, i.e.:
I've found only one book that provides a (partial) derivation of this formula: "A Biostatistics Toolbox for Data Analysis" by Steve Selvin. He uses g-bar (I don't know how to write that here) to stand for the weighted mean effect estimate and g-hat-sub-i (again, I don't know how to write that here) to stand for each (unweighted) effect estimate. He then gives the following partial derivation:
I think I understand some of the steps in this derivation but it would be great if the reasoning (i.e. variance algebra/rules) for each step could be spelt out. For example, how do we get the first step/line of the derivation:
It seems he's using the fact that a/b is the same as a x 1-over-b. But what rules of "variance algebra" is he relying on to get that first squared term
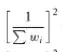 ?
Thank you so much for your help
?
Thank you so much for your help
Thank you very much!
Best Wishes
Adam