Interpreting the plot of residuals for a cox proportional-hazards model and informative censoring

Question

I would like to use a cox proportional hazards model to estimate the effect of percent tree cover on the minimum time interval between the occurrence of two species at a location. The first species I consider at each location is the domestic dog, and the second is the coyote.

The arrival of a coyote after a dog, after a certain time limit, is the "event" for my model. Since I am interested only in the visit of the first coyote after a dog, I censored all dog "waiting times" for dogs who were eventually followed by another dog instead of a coyote.

I'm using only one continuous covariate for my model (%tree cover), but unfortunately, I only have four different values for it across all my time-to-events. Additionally, the large abundance of dogs relative to coyotes results in a very high 95% censoring rate.

The assumptions of proportionality and linearity appear to hold for my model, based on the Schoenfeld test (with cox.zph()) and a plot of Martingale residuals against my covariate values (ggcoxfunctional()).

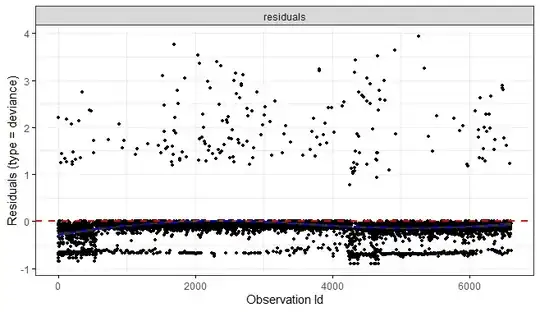
However, I have plotted the deviance residuals for my model and obtained the following plot:

We can see that all the events have high positive residuals, while the censored observations are clustered around 0. Low residuals are expected for censored observations. However, I suspect there was also informative censoring because dogs are very common during the day while foxes appear only at night. Hence, censored dogs actually would have a lower probability of being followed by a fox.

Is there a way I can account for this with a Cox model? Or would this approach not be appropriate for my data?

Answer 1

I'll start with the questions you raise, but then address what might be a bigger problem in your analysis.

Therneau and Grambsch said the following about deviance residuals over 20 years ago:

The deviance residual was designed to improve on the martingale residual for revealing individual outliers, particularly in plotting applications. In practice it has not been as useful as anticipated.

I don't think much has changed since then, so I don't see that deviance-residual plot to be of concern itself. As you note, this is what you expect with a high fraction of censoring. In general, the scaled Schoenfeld residuals (for evaluating proportional hazards, PH) and martingale residuals (for evaluating functional form) are more important.

The lack of PH when you incorporated time of day as a continuous predictor in your model could represent an improper functional form. Time of day is tricky, as you need to deal with the equivalence of 00:00 and 24:00 hr (0 and $2 \pi$). You could consider incorporating it as a circular predictor via sine and cosine terms. If you want to proceed that way, see this page and this answer for a start.

When you dichotomized time into coyote-rich and coyote-poor periods, you say that the dichotomized predictor then violated PH. If you're not interested in time of day as a predictor and just want to use it to control for coyote/dog prevalence, you could include the dichotomized times as strata instead. That's a standard way to deal with lack of PH for a categorical predictor. You can even include strata by covariate interactions, if you think that the effect of tree cover will differ between those time-of-day strata.

A potentially bigger problem is whether your use of survival analysis and censoring this way makes sense in your study. Unless you have reason to believe that each coyote was attracted to the plot by an individual dog, you might just be sampling from independent distributions of dog and coyote arrival times, as functions of tree cover and time of day. Or perhaps the probability of coyote arrival depends on the number of dogs in the area rather than the time that the last dog happened to arrive. You might still find that your "survival" model "fits" the data, but you might be missing the real story.

Make sure that you first evaluate in detail how the appearance times of dogs and coyotes each are associated with time of day and tree cover. Also, examine what would happen if you applied your survival analysis to randomly generated independent dog and coyote arrival times that match the general characteristics of your data. Your survival analysis might just be a complicated way to describe something that has a much simpler interpretation.