I recently encountered a problem of overconfidence in Bayesian linear regression. The initial thread can be found here. I recall the basic equations of Bayesian linear regression here for clarification.
Data: $D:=\{X, Y\}, X \in \mathbb{R}^{n_d \times n_x}, Y \in \mathbb{R}^{n_d \times 1}, n_d: \text{Number of data points}, n_x: \text{Dimension of input}$.
Model: $p(y | x, \theta) = \mathcal{N}(\phi(x)^T\theta,\sigma_n^2), \theta: \text{Linear model parameters}, \phi(x):\mathbb{R}^{n_x} \mapsto \mathbb{R}^{n_{\theta}} \text{ is the feature mapping}$.
Likelihood: $p(Y | X, \theta) = \mathcal{N}(\Phi(X)\theta, \sigma_n^2I_{n_d}), \Phi(X) \in \mathbb{R}^{n_d \times n_{\theta}}: \text{Matrix of data points features}$.
Prior: $p(\theta)=\mathcal{N}(\mu_0, \Sigma_0)$.
Posterior (via Bayes): $p(\theta | D) = \frac{p(D | \theta)p(\theta)}{\int{p(D|\theta)p(\theta)}d\theta} = \mathcal{N}(\mu_D, \Sigma_D)$.
Predictive distribution: $p(y|X,D) = \int{p(y|x,\theta)p(\theta|D)d\theta} = \mathcal{N}(\phi(x)^T\mu_d, \sigma_n^2+\phi(x)^T\Sigma_D\phi(x))$
I figured out that for my problem of the previous thread it would be better to maximize the likehood of the predictve distribution instead of using the Bayesin linear regression framework. To be more precise I solved the following optimization problem.
$p(\theta) = \mathcal{N}(\mu_{\eta}, \Sigma_{\eta}), \eta:=(\mu_{\eta}, \Sigma_{\eta})$.
$p(y|x) = \int{p(y|x,\theta)p(\theta)d\theta} = \mathcal{N}(\phi(x)^T\mu_{\eta}, \sigma_n^2+\phi(x)^T\Sigma_{\eta}\phi(x))$.
$\eta^* = \arg \max_{\eta} p(Y | X)$.
The resulting model is much more informativ about its confidence of the assumed basis functions. If the basis functions are choosen correctly the predictive distribution fits very nicely to the data points. However, if there are crucial basis functions are missing, the uncertainty of the predictive distribution becomes very high.
Some question I have regarding my approach:
- Under which terms I can find more information in literature about my approach? Is it a form of distribution fitting?
- What does it actually mean to maximize the likelihood of the predictive distribution in connection with Bayesian linear regression? Is there a way to incorperate prior knowledge about $p(\theta)$? I have something in mind like a additional penalty term that does depend on the KL-divergence between $\mathcal{N}(\mu_0, \Sigma_0)$ and $\mathcal{N}(\mu_{\eta}, \Sigma_{\eta})$.
- The objective function seems to be multimodal with many local optima. Whats the best way to overcome a local solution?
Edit: Example:
Assuming the same setting from here, we got the ground truth function
$f_1(x) = a_1 + a_2 x + a_3 x^2, \text{with } a_1 = 1, a_2 = 2, a_3 = 3,$
from which we sample $10$ data points randomly. Lets look at the result from the optimization approach, if we assume that our model has the same terms like the ground truth (best case scenario).
The predictive distributuon fits perfectly to the data points (just like expected). The mean and covariance (i assumed independence of the parameters) are
$\mu_{\eta} = [1, 2.3, 2.7]^T, \Sigma_{\eta} = 1\mathrm{e}{-13} \text{diag}(1, 1, 1)$.
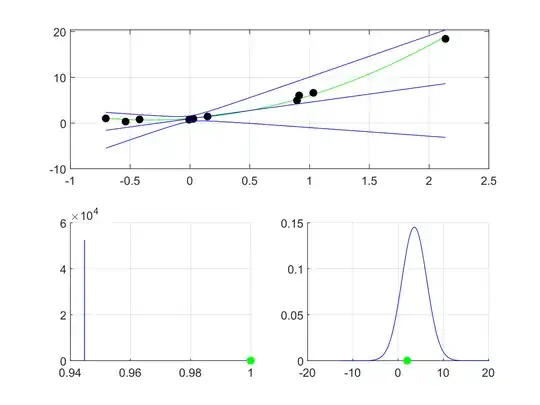
In the second case we assume a trimmed model of the form
$f_2(x) = b_1 + b_2 x$.
Optimization then yields
with mean and covariance
$\mu_{\eta} = [0.94, 3.59]^T, \Sigma_{\eta} = \text{diag}(0, 7.5)$.
In comparison to Bayesian linear regression there is no overconfidence to be observed. I think that the predictive posterior fit looks pretty good and matches with my expectations. Surprisingly, the constant term b_1 is equal to the ground truth one a_1. I wonder if this happened by accident or by construction.