0

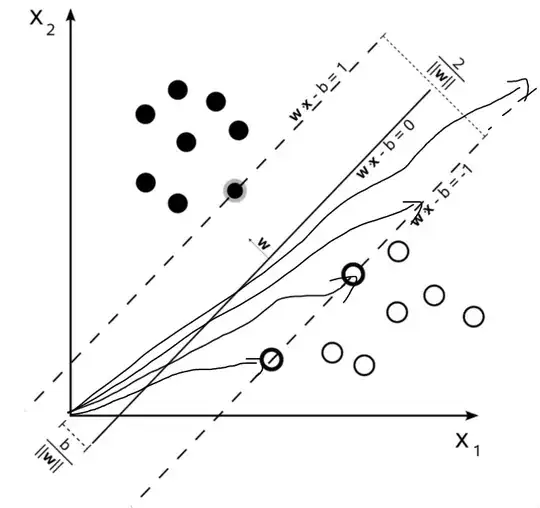
So given the picture and the related definitions from this answer:

enter image description here

How does the equation $\textbf{w} \cdot \textbf{x}^{(i)} - b = -1$ hold for several vectors $\textbf{x}^{(i)}$ when $\textbf{w} \cdot \textbf{x}^{(i)}$ is the dot product?

I can see that a $b$ can be chosen that it might be true for one vector but what if there are a lot of points to fulfill this like I have drawn here (every drawn line represents a vector)

enter image description here

  • So the values of the dot product will differ a lot depending on where my points on the support lines are located and reach $0$ at infinty.
  • So there will be a lot for different $b_i$ to be chosen but that's not the defintion.

I am just not able to make sense of the definition. What crucial point am I missing here?

kjetil b halvorsen
  • 63,378
  • 26
  • 142
  • 467
OuttaSpaceTime
  • 135
  • 4
  • 1
    I found out that is basically comes down to how a plane can be discribed given it's normal vector how it is shown here [here](https://www.youtube.com/watch?v=gw-4wltP5tY&t=52s) – OuttaSpaceTime Feb 07 '22 at 18:15

0 Answers0