The question concerns a non-parametric estimation of a finite population distribution based on a random sample (without replacement) comprising an appreciable fraction of that population.
The empirical cumulative distribution function (ECDF) is a fine non-parametric estimator. It estimates the proportion of the population at or below any number $x$ to be the proportion in the sample at or below $x.$
Ordinarily, for a sample with replacement, one would use the Kolmogorov Distribution to construct confidence bands around the ECDF. These bands are obtained by raising and lowering the graph of the ECDF by an amount $D,$ the critical value of a KS test. For $100(1-\alpha)\%$ confidence, $D$ is the $1-\alpha$ quantile of the Kolmogorov distribution, divided by $\sqrt{n}.$ (The bands obviously can be cut off by $1$ at the top and $0$ at the bottom, as shown in the figures below.)
A standard correction factor for estimating standard errors of the mean in large samples of size $n$ without replacement from populations of size $N$ is to multiply them by $\sqrt{(N-n)/(N-1).}$ See our explanation at Explanation of finite population correction factor?.
As an ad hoc attempt at a solution, I have adjusted the critical value of $D$ in the same way. Simulations indicate this adjustment works provided $N$ is large -- typically over a thousand or so. "Works" means that the bands are at the proper distances to achieve the intended confidence level.
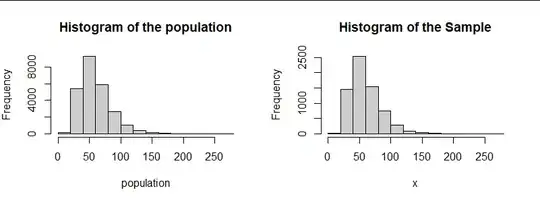
The first figure shows a skewed population characteristic of incomes. It has $25,000$ values. At the right of that figure is a histogram of a random sample of size $6,750$ (without replacement) from that population. (Comments to the question indicate these are the quantities the OP actually has.) Because it's a large sample, its histogram has almost the same shape as the population histogram.
The next figure shows the ECDF (at left) for the sample with the 95% confidence bands (as adjusted for the finite population). It's hard to distinguish the ECDF itself (in black) from the bands, so at the right I have plotted the difference between the sample ECDF and the population ECDF. When the red and blue lines at the right are set at the correct heights, then in 95% of such random samples, the entire black graph of deviations will lie between those bands. Thus, although in practice we never know the population distribution, when we look at the left plot (which is based only on information about the sample), we get a good sense of how reliably that sample represents any quantile of the population.

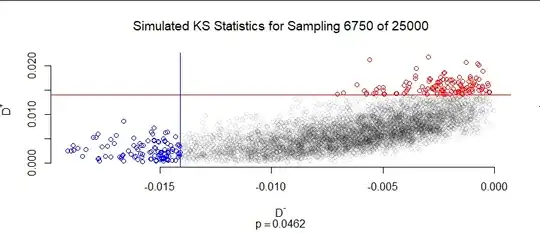
For the final figure I have created five thousand random samples of the same population (a quantity I could generate and analyze in a couple of seconds). For each one I recorded the largest positive deviation relative to the population distribution, $D^+,$ and the greatest negative deviation, $D^-.$ (The KS statistic is the larger of $D^+$ and $-D^-.$) Thus, each sample contributes on point $(D^-, D^+)$ to this plot. Samples where one (or potentially both) deviations fell beyond the confidence bands are shown in red and blue. As noted at the bottom, this is $0.0462 = 4.62\%$ of all the samples. Because this number is so close to $5\%,$ we may conclude that the method of computing the critical value of $D$ is accurate.
The method I used is shown in the code below. It calculates the critical value of $D$ by (a) implementing the CDF of the Kolmogorov distribution, (b) inverting it with a root finder, and (c) applying a correction recommended in the Wikipedia article. The correction makes little difference for a sample of this size, but helps a little bit for smaller samples. Once the sample size drops down to the hundreds, though, these calculations are too conservative in the sense that their critical value is too large; equivalently, the actual confidence of this test is higher than its nominal level.
You can change obvious parts of this code to study any sampling situation you might face. Two things to bear in mind are (1) obtaining tied values in the sample should be a rare event and (2) other than that, it doesn't matter what you assume for the population distribution.
#
# The Kolmogorov CDF.
#
pK <- Vectorize(function(x) {
x <- pmin(4, pmax(2^(-4), x))
kmax <- ceiling(3 * x)
k <- seq(1, 2*kmax-1, by=2)
sum(exp(-(k * pi / x)^2 / 8)) * sqrt(2*pi) / x
})
#
# The percentage point function (inverse CDF)
#
qK <- Vectorize(function(q, ...) {
q <- pmax(1e-13, pmin(1 - 1e-13, q))
f <- function(x) pK(x) - q
uniroot(f, c(2^(-4), 4), ...)$root
})
#
# An adjustment to make `pK` more accurate for smaller `n`.
#
adjust <- function(x, n) (x - 1/sqrt(36*n)) / (1 + 0.25/n)
#
# An example.
#
N <- 25e3
n <- 6.75e3
alpha <- 0.05
population <- exp(rnorm(N, 4, 0.4))
#
# Compute some objects for the plots.
#
F.0 <- ecdf(population)
D <- adjust(qK(1-alpha), n) / sqrt(n) * sqrt((N-n)/(N-1))
#
# Sample from the population.
#
set.seed(17)
x <- sample(population, n)
F.x <- ecdf(x)
par(mfrow=c(1,2))
#
# Figure 1: histograms.
#
hist(population, col=gray(.8), main="Histogram of the population")
hist(x, col=gray(.8), main="Histogram of the Sample")
#
# Figure 2: how the confidence bands work.
#
plot(range(x), 0:1, type="n", bty="n", yaxp=c(0, 1, 2),
main="Sample Distribution", xlab="Income", ylab="Proportion Below")
x.0 <- seq(min(x), max(x), length.out=201)
y <- F.x(x.0)
polygon(c(x.0, rev(x.0)), c(pmin(1, y+D), pmax(0, rev(y)-D)), col=gray(.80), border=NA)
# curve(F.x(x), add=TRUE, lwd=2, n=201)
curve(F.x(x), add=TRUE, n=501)
curve(pmin(1, F.x(x) + D), add=TRUE, col="Red", n=501)
curve(pmax(0, F.x(x) - D), add=TRUE, col="Blue", n=501)
plot(range(x), 2*D*c(-1,1), type="n", bty="n", xlab="Value", ylab="Deviation",
main=bquote(paste(.(100*(1-alpha)), "% Confidence Interval")))
abline(h = D*c(-1,1), col = c("Blue", "Red"))
curve(F.x(x) - F.0(x), min(x), max(x), add=TRUE, n=501)
par(mfrow=c(1,1))
#------------------------------------------------------------------------------#
#
# A simulation.
#
N <- 25e3 # Population size
n <- 6.75e3 # Sample size
alpha <- 0.05 # Test size: confidence is 100*(1-alpha).
set.seed(17)
population <- exp(rnorm(N, 4, 0.4))
F.0 <- ecdf(population)
#
# Draw samples repeatedly and compare their ECDFs to the population CDF.
#
sim <- replicate(5e3, {
x <- sort(sample(population, n))
y <- (1:n) / (n+1) - F.0(x)
range(y)
})
#
# Assess and plot the results.
#
D <- adjust(qK(1-alpha), n) / sqrt(n) * sqrt((N-n)/N)
p <- mean((ilow <- sim[1,] < -D) | (ihigh <- sim[2, ] > D))
plot(t(sim), bty="n", col=ifelse(ilow, "Blue", ifelse(ihigh, "Red", "#00000020")),
main=bquote(paste("Simulated KS Statistics for Sampling ", .(n), " of ", .(N))),
sub=bquote(p==.(signif(p, 3))),
xlab=expression(D^paste("-")), ylab=expression(D^paste("+")))
abline(h = D*c(-1,1), v = D*c(-1,1), col=c("Blue", "Red"))


