Related scattering theory and free path length
Change frame of reference
You can compute your method 1 more easily by switching the frame of reference to a co-moving frame along with the stream of cars.
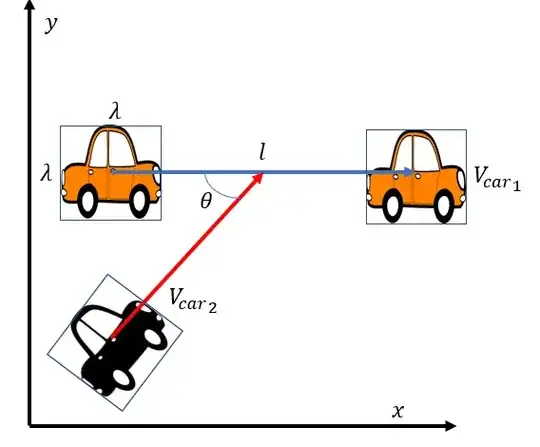
If the car 1 has the velocity $\vec{v}_1$ and car 2 have the velocity $\vec{v}_2$ then in the co-moving frame the relative speed between the cars is $\vec{u} = \vec{v}_1 - \vec{v}_2$ with the components
$$\begin{array}{}
u_{x,2} &=& v_2 \text{cos}\,\theta -v_1 \\
u_{y,2} &=& v_2 \text{sin}\, \theta \\
\end{array}$$
Then we consider a different angle $\theta^\prime$ at which the car2 is passing the stream while the cars 2 are standing still. This angle is related to the new vertical and horizontal velocities in the co-moving frame of reference.

In 'Motivation for the choice of integral bounds' you work with two components:
The probability of the car 1 hitting car 2, which relates to $u_{x}$ the relative horizontal speed at which car 1 approaches car 2.
The probability of the car 2 hitting car 1, which relates to the $u_{y}$ the relative vertical speed at which car 1 crosses the stream.
In the viewpoint of the frame of reference that is co-moving with the cars 1, you can see that this idea of two components 'car 1 hitting car 2' and 'car 2 hitting car 1' is confusing. One should not add the horizontal and vertical components $u_{x}$ and $u_{y}$ together (which is like computing the Manhattan distance), but you should use the Euclidian measure for the distance traveled by car 2 relative to the cars in the stream $\sqrt{u_{x}^2 + u_{y}^2}$.
Effective cross-section
To compute the collision rate or collision probability, you will have to consider the effective cross-section of the car moving through the stream.
If you would do this accurately you will have to determine the distances $d_1$ and $d_2$ which are the distances between the point where the two cars are just touching and lines through the centers of the two cars, these lines are drawn in the direction of travel.
To compute these distances is a bit annoying and you have to consider both the angles $\theta$ and $\theta^\prime$. And, there are different cases, for instance, car 2 might hit the other car on the left or the right side depending on the angle.
You could approximate the distance with $\lambda$ if you simplify the shape of the cars as spheres with diameter $\lambda$. The cross section will then be twice this distance because the car 2 can hit the car 1 on the left and on the right.
The distance between the cars 1 or the density in the stream.
If we approach the stream at an angle than the distance between the cars in the stream becomes smaller. In the figure below you see that this distance is not $l$ but instead $l \sin \, \theta^\prime$.

Probability of hit with method 1
The probability that a car 2 hits another car in the stream is then
$$\frac{\text{cross-section}}{\text{path-width}} \approx \frac{2 \lambda}{l \cdot \sin \, \theta^\prime}$$
and with $$\sin \theta^\prime = \frac{u_{y}}{\sqrt{{u_{x}}^2+{u_{y}}^2}}$$
we can rewrite it as
$$\frac{\text{cross-section}}{\text{path-width}} \approx
\frac{2 \lambda}{l} \sqrt{ 1 + \left( \frac{v_2 \cos \, \theta - v_1}{v_2 \sin \, \theta} \right)^2}$$
It is possible that this ratio becomes larger than 1 when the cross-section becomes larger than the path width. In that case a collision is certain (if the cars in the stream are with constant distance/gaps in between).
Method 2, using density
With the method you will have to compute the area that is swept by car 2 and integrate over that area the density of the cars 1 (which is more easy if this density is constant).

Note that the angle of the path changes the area of the path. The integral that you compute, and the motivation for it, is not so clear. It is like you are computing the area of the path of a 1 dimensional line. That area is not dependent on the angle of the car 1. But, it is wrong to use a line. You need to consider the entire block.
See in the image below how car 2, if it would be taking an alternative path, would sweep a different area of the stream. Also the velocity of cars 1 plays a role because they change the effective angle $\theta^\prime$ which will change the size of the area that the car 2 sweeps through the stream.
Note: in the image $\cos \theta^\prime$ should be $\sin \theta^\prime$. This will be edited later.
The image above depicts a stream of uniform density, but you can also consider a nonuniform density in which case you perform an integration over infinitely small slabs.
So this area is equal to
$$w \cdot x = w \cdot \frac{2\lambda}{\sin\, \theta^\prime}$$
You will have to multiply by the density of the cars which is 1 car per block of size $w$ by $l$, ie $\rho = 1/(l\cdot w)$ and you will end up with the same expression as method 1.
$$w \cdot x \cdot \rho = w \cdot \frac{2\lambda}{\sin\, \theta^\prime} \cdot \frac{1}{l\cdot w} = \frac{2\lambda}{l \cdot \sin\, \theta^\prime} $$
Method 2 variant
We can also compute the integral from method 2 in the stationary frame of reference.
The area computed above is using the area of the parallelogram as (height times width). This can be done in two ways:
- one is $w \cdot x$ where $w$ is the width of the stream and $x$ the length of the intersection.
- Another way would be to multiply the cross-section $2\lambda$ with the length of the path which is depending of the width of the stream and the angle $\theta^\prime$.
This length of the path can be seen as an effective velocity relating how many area the car 2 effectively travels in the co-moving frame of reference of the car 1 stream.
Instead of computing the area in the frame of reference of the co-moving frame we could also compute the area in the stationary frame of reference.
In the stationary frame of reference the distance traveled is $$\Delta x \cdot \text{cross-section} = v_2 \Delta t \cdot \text{cross-section}$$
In the co-moving frame of reference the distance traveled is $$v_{effective} \Delta t \cdot \text{cross-section}$$
So we could compute the effective area as the area in the stationary frame of reference multiplied by a factor
$$v_2 \Delta t \cdot \text{cross-section} \cdot \frac{v_{effective}}{v_2}$$
This factor at the end is the ratio of the difference in speeds of car 1 and car 2 in the numerator and the speed of car 1 in the denominator
$$ \frac{v_{effective}}{v_2} = \frac{\sqrt{(v_2 \cos \, \theta -v_1)^2+(v_2 \sin \, \theta)^2}}{v_2}$$
The time traveled in the stream of width $w$ is relating to another factor
$$\Delta t = \frac{w}{v_2 \sin \, \theta}$$
If you put those together you get the same result again.
If you like to compute an integral to account for some nonhomogeneous density then you could use a path integral
$$ \int \text{cross-section}(s) \rho(s) \frac{|\vec{v}_1(s)-\vec{v}_2(s)|}{|\vec{v}_2(s)|} \text{d}\, s$$
Where the velocities are now considered as vectors $\vec{v}_1$ and $\vec{v}_2$, and the vertical bars $|\cdot|$ denotes the magnitude.
If the cross-section $2 \lambda$, density $\rho = \frac{1}{l\cdot w}$ and speeds are constant then we can take them outside of te integral and we end with
$$ \begin{array}{}
\text{cross-section} \cdot \rho \cdot \frac{|\vec{v}_1-\vec{v}_2|}{|\vec{v}_2|} \cdot \int \text{d}\, s &=& \overbrace{\left(2 \lambda\right)}^{\text{cross-section}} \cdot \overbrace{\left( \frac{1}{l \cdot w} \right)}^{\text{density}} \cdot \overbrace{\left(\frac{|\vec{v}_1-\vec{v}_2|}{|\vec{v}_2|}\right)}^{\text{velocity factor}} \cdot \overbrace{\left( w \frac{|\vec{v}_2|}{{v}_{2,y}} \right)}^{\text{path length $\int \text{d}s$}} \\
&=& \frac{2 \lambda}{l} \frac{|\vec{v}_1-\vec{v}_2|}{{v}_{2,y}} \\
&=& \frac{2 \lambda}{l} \frac{\sqrt{(v_2 \sin \theta)^2 + (v_2 \cos \theta- v_1)^2}}{v_2 \sin \theta}
\end{array}$$
Note that this gives the average number of collisions. The meaning of an average is different depending on the distribution of the cars in the stream. (See: What distribution to use to model time before a train arrives?)
In your final application with airplanes you might consider the collisions between two streams. Then you can have an integral over the space and use the concentrations of both streams
$$ \iint \rho_1(x,y) \rho_2(x,y) \text{cross-section}(x,y) {|\vec{v}_1(x,y)-\vec{v}_2(x,y)|} \text{d}x \text{d} y $$
which gives the rate of collisions per second.
You could in addition take into account variations in the speeds at given positions $x,y$ and compute the average of the factor $\text{cross-section}(x,y) {|\vec{v}_1(x,y)-\vec{v}_2(x,y)|}$.

 Basically at rach dt, we integrate the probability of a car1 beeing on the blue line and on the red line.
Basically at rach dt, we integrate the probability of a car1 beeing on the blue line and on the red line.