0

I am practicing hierarchical clustering and I am having doubts about the interpretation of dendrogram height. Let's take the code in example with points (1,1), (2,2), (5,5), (9,9), (10,10), and (13,13).

X = [1 1; 2 2; 5 5; 9 9; 10 10; 13 13];

P = pdist(X, 'squaredeuclidean');
S = squareform(P);
L = linkage(S, 'ward');
figure(1); H = dendrogram(L);

figure(2)
hold on
for i = 1:1:size(X, 1)
    scatter(X(i, 1), X(i, 2))
    text(X(i, 1)+0.3, X(i, 2)+0.3, int2str(i))
end

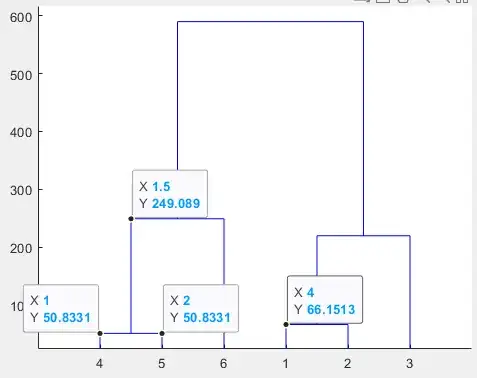
The result dendrogram is:

enter image description here

Calculating the squaredeuclidean distance of only points (1,1) and (2,2), the value is 2 (pdist2([1 1], [2 2], "squaredeuclidean"). And this distance is also the distance of points (9,9) and (10,10).

Now, I know that the height of the dendrogram represents the order in which the elements are joined in the cluster, and so points (9,9) and (10,10) (points 4 and 5) are joined first, and then points (1,1) and (2,2) (points 1 and 2) because the height of the first one is lower. But shouldn't the height (50.8331) shown in the dendrogram correspond to the distance between point 4 and point 5, a distance equal to 2? I think I'm getting confused. Also because all the other heights don't match the definition of Euclidean squared distance.

Last doubt. Does the height of the dendrogram represent inter-cluster deviance (between two different clusters) or intra-cluster deviance (the deviance of points in a cluster)? I need to calculate the deviance lost from clustering and this is equal to the ratio of the inter-group deviance to the total deviance, the height which of the two represents?

Thanks to all.

Orla098
  • 1
  • 1

0 Answers0