Background
I have measurements of a trajectory that is parameterized by time. The data consists of points with two spacial coordinates $(\tilde{x}_i, \tilde{y}_i)$ and a time stamp $(t_i)$. I'm using numpy.polyfit to fit a 2nd order polynomial to the data:
Since the data describe the motion of a physical object in 2D space, the parameters from the polynomial represent the velocity and acceleration of the object (and initial position).
Question
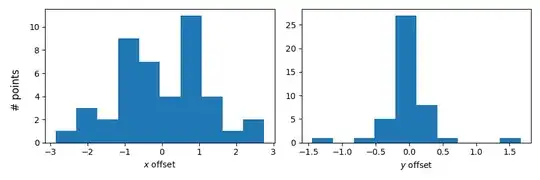
My data points (of course) do not perfectly fit the model, thus there are residuals in $x$ and $y$ (i. e. the measured coordinates have some offset from where they should lie according to the fit at the corresponding time):
Because the derived velocity and acceleration are important quantities for me, I came up with the following system to test how reliable they are:
- I assume that the curve from the fit truely represents the actual trajectory, and that my measured data points $(\tilde{x}_i, \tilde{y}_i)$ only deviate from the true locations $(x_i, y_i)$ by a gaussian offset:
$\begin{pmatrix} \tilde{x}_i\\ \tilde{y}_i \end{pmatrix} = \begin{pmatrix} x_i\\ y_i \end{pmatrix} + \begin{pmatrix} \delta_{x, i}\\ \delta_{y, i} \end{pmatrix}$
- Based on this assumption, I create fake data sets $(\hat{x}_i, \hat{y}_i)$ by adding some random offset drawn from gaussian distributions that have the same standard deviations ($\sigma_x$, $\sigma_y$) as the offset distribution of the measured data:
$\begin{pmatrix} \hat{x}_i\\ \hat{y}_i \end{pmatrix} = \begin{pmatrix} x_i\\ y_i \end{pmatrix} + \begin{pmatrix} \hat{\delta}_{x, i}\\ \hat{\delta}_{y, i} \end{pmatrix}$
If I'm not mistaken, this should mean that the real dataset is basically indistinguishable from the genrated ones.
I then fit polynomials to the generated data sets and compare the velocity and acceleration vectors to those of the measured data. Note that in the plots below, the black outline indicates the vectors of the measured data, while the semi-transparent blue ones are from the generated data. The gray dashed lines indicate the mean values. (The vectors are warped due to non-square aspect ratios.):
For these velocities and accelerations I would then calculate the standard deviations and use them as error estimates for the measured values. Is that reasonable? Or am I commiting some kind of fallacy? I'm suspicious because the vectors from the measured data are awefully close to the mean values.
Also, I guess this counts as a Monte Carlo simulation. Is that correct?
Additional Note
The numpy.polyfit function can also provide diagnostic information like the covariance matrix and singular values of the scaled Vandermonde coefficient matrix, and I would guess that they can also tell me similar things, however I'm not exactly sure because I don't really know what they mean (see also link, link).