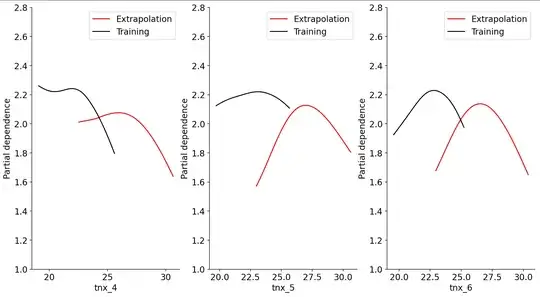
I trained a Multilayer Perceptron to predict a variable Y based on a set of predictors. Then I decided to test it on unseen data outside of the training range. I am aware of (some of) the implications of extrapolating machine learning models, and how ANN specifically can lead to crazy extrapolations. Nevertheless, my experiment requires this step, and I believe the shape the MLP produces when out of range is not necessarily the issue.
The issue, as seen in the partial dependence plot below, is that I would expect the extrapolation (red curve) to follow the down slope of the training curve (black curve). Instead, what we see is an almost identical curve, but translated to the right of the training curve. I would appreciate any insights on why this is happening, or any comments suggesting there is one or more flaws on my logic. Lastly, it would be interesting to hear thoughts on how to achieve this "extension" of the training curve on to the extrapolation curve.
def create_model():
model = Sequential()
model.add(Dense(200, input_dim=len(X_train.columns)))
model.add(Activation('relu'))
model.add(Dropout(0.1))
model.add(Dense(200))
model.add(Activation('relu'))
model.add(Dropout(0.1))
model.add(Dense(200))
model.add(Activation('relu'))
model.add(Dropout(0.1))
model.add(Dense(200))
model.add(Activation('relu'))
model.add(Dropout(0.1))
model.add(Dense(1, activation='linear'))
# compile the keras model
model.compile(loss='mean_absolute_error', optimizer=tf.keras.optimizers.Adam(0.001), metrics=['mean_squared_error','mean_absolute_error'])
return model
model_rf = Pipeline([
('scaler', StandardScaler()),
('estimator', KerasRegressor(model=create_model, epochs=200, batch_size= 1024, verbose=1))