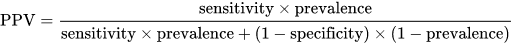Probability of having disease given positive test result

Question

I am trying to solve a puzzle and have struck in some fundamental concepts of probability. In an epidemic, its found that only one in 10000 people actually suffer from the rare disease. So the probability that I am positive will be

P1= 1/10000

But there is a medical test also which has 99% accuracy. Unfortunately my test result is positive. As per this test, the probability that I am positive will be

P2= 99/100

Now I have two probabilities P1 and P2. The first question that comes to my mind is how can we have two probabilities for a single event (i.e. being "positive")? Why they are different? Secondly, which one should I trust and why ? Or what is the actual probability of me being found positive?

Edit The specific question is if 100000 people are tested, and the test says I am positive, then what is the probability that I am actually suffering from the disease given the test results?

Answer 1

The question is not so basic as it may seem.

It concerns the notion of pre-test and post-test probability. Assuming that both these probabilities P1 and P2 were given to you by the test lab, and are not implied by somebody else, here's how they relate to each other.

P1 is a prevalence metric, it tells you how likely it is that a random person has a disease without knowing anything about the person.

P2 is the probability that you have the disease given that you tested positive. Again, here I'm assuming that you got P2 from the lab explicitly. This is important because you may have found the accuracy 99% somewhere and simply assumed that it's the probability. This would have been wrong as explained further.

This example has relevant equations. Here's how it works. A test has a sensitivity and specificity, i.e. how well it can classify positive and negative cases. These two metrics give you positive test likelihood ratio as $$R=\frac{sensitivity}{1-specificity}$$ Using P1 you obtain pretest odds, before knowing anything about your lab result the odds of having a disease are:$$\pi=\frac{P1}{1-P1}$$ Now you can calculate the post test odds, i.e. odds of having disease after lab results came back positive:$$\pi_p=\pi R$$ Finally we convert post-test odds into probability:$$P2=\frac{\pi_p}{1+\pi_p}$$

You can see how the pre-test probability P1 enters into post-test probability P2. However, it is not possible to work the numbers out because we need to know sensitivity and specificity of the test for that. Knowing only the accuracy of the test is not enough for that. You can lookup the definition of accuracy metric and see that yourself. Reported Accuracy of the tool also depends on prevalence of disease in the test population.

Notice how dramatically changes the probability of having disease post test, i.e. after receiving the lab result. It is because the test has a good discriminating ability.

Answer 2

Both existing answers are absolutely right here, but I thought I might be able to make this a little more intuitive.

1. The base rate is the prior probability

If one in 10,000 people have the disease (this is called the base rate, or prevalence), the probability of any random person, about whom we have no other information, having the disease is $\frac{1}{10000} = .0001$. That's also the probability that you have it, before you take a test or check whether you have symptoms.

2. Accuracy is complicated

It doesn't make sense to talk about a test being accurate or not in general terms. Instead, you can talk about the sensitivity of the test (probability of being positive when taken by people who do in fact have the disease) and the specificity (probability of being negative when taken by people who do not have the disease). There's no reason to expect these probabilities to be the same. (See wikipedia for more).

3. Putting it all together

You want to know the positive predictive value: the probability of having the disease, given that your test is positive. You need to know the base rate/prevalence, sensitivity, and specificity to calculate this, and the equation is on Wikipedia:

In short (because the other answers cover this well), you want to figure out how how many people have the disease and get positive tests (true positives), and how many people don't have the disease but get positive tests (false positives), and use this to calculate what proportion of all the people with positive tests are true positives.

Answer 3

The idea of these types of questions/puzzles is to apply some Bayesian analysis and use the test result to update the probability that you are sick.

The people that got a positive test result are

• either sick and got a correct test result
• or not sick and got an incorrect test result.

The ratio of those two cases are the odds for being sick.

---

For example. Say 1 000 000 people do the test and the outcome is:

$$\begin{array}{} & \text{sick} & \text{not sick} & \text{total} \\ \text{positive test}& 99 & 9999 & 10098 \\ \text{negative test}& 1 & 989901 & 989902\\ \text{total} &100 &999 900 & 1000000 \end{array}$$

Here we see that among the sick people 99% test positive and among the not sick people 99% test negative.

If you have a positive test then you are one of the 10 098 people with a positive test, but only 99 among those are truly sick. So you have $\frac{99}{10098} \approx 0.98\%$ probability of being sick.

---

So your problem is to make that table. Below this is done stepwise

• Fill in the total amount of people $n$ (the actual value does not matter, it will drop from the equation eventually)$$\begin{array}{} & \text{sick} & \text{not sick} & \text{total} \\ \text{positive test}& & & \\ \text{negative test}& & & \\ \text{total} & & & n \end{array}$$

• The prior distribution sick is $p=0.0001$, you can fill this into the totals $$\begin{array}{} & \text{sick} & \text{not sick} & \text{total} \\ \text{positive test}& & & \\ \text{negative test}& & & \\ \text{total} & p n & (1-p) n & n \end{array}$$

• If you know the probability distribution of the test result/outcome given the state sick/not-sick, then you can fill in the rest of the table.

  If a fraction $x$ of the sick people have a positive test $$\begin{array}{} & \text{sick} & \text{not sick} & \text{total} \\ \text{positive test}& x p n & & \\ \text{negative test}& (1-x) p n & & \\ \text{total} & p n & (1-p) n & n \end{array}$$

• If a fraction $y$ of the non sick people have a negative test $$\begin{array}{} & \text{sick} & \text{not sick} & \text{total} \\ \text{positive test}& x p n & (1-y) (1-p) n & \\ \text{negative test}& (1-x) p n & y (1-p) n & \\ \text{total} & p n & (1-p) n & n \end{array}$$

• We can complete the totals on the right $$\begin{array}{} & \text{sick} & \text{not sick} & \text{total} \\ \text{positive test}& x p n & (1-y) (1-p) n & x p n + (1-y) (1-p) n \\ \text{negative test}& (1-x) p n & y (1-p) n & (1-x) p n + y (1-p) n\\ \text{total} & p n & (1-p) n & n \end{array}$$

Then the probability to be sick given a positive test result is

$$\begin{array}{} P(\text{sick} | \text{positive test}) &=& \frac{x p n }{x p n + (1-y) (1-p) n} \\ &=& \frac{xp }{xp + (1-y)(1-p) } \\ & = & \frac{x }{xp + (1-y)(1-p) }p \end{array}$$

---

In your problem, it is only stated that the accuracy is 99%. This is not a very complete description. The detection can make two types of errors a sick person with a negative test, and a not sick person with a positive test. The ratios of these two can be different.

In some of these problem statements, it is plainly just stated that the accuracy is 99% (like in your problem/puzzle), and implied that the false positive and false negative rates are the same and 1%. This implication is not correct/accurate but if you ignore this error in the question then you can say $x = y = 0.99$ and solve the above equation

$$\begin{array}{} P(\text{sick} | \text{positive test}) &=& \frac{x }{xp + (1-y)(1-p) }p \\ &=& \frac{0.99 }{0.99 \cdot 0.0001 + 0.01 \cdot 0.9999 } 0.0001\\ &=& \frac{0.99 }{ 0.010098 } 0.0001 & = & 0.009803922 \end{array}$$