11

Can we say that the value of the cumulative distribution function at the mean F(X< Mean) is always 0.5 for all kind of distributions (even ones that are not symmetric)?

BCLC
  • 2,166
  • 2
  • 22
  • 47
Velicious
  • 121
  • 5

4 Answers4

25

No, this is false. That point is the median, and it is not equal to the mean in all cases, for example, an exponential distribution.

$$ X\sim \exp(1)\\ \mathbb E[X]=1\\ \operatorname{median}(X)=\log 2\approx 0.69 $$

We can simulate this in software, such as R.

set.seed(2021)
X <- rexp(10000, 1) 
mean(X) # approximately 1
median(X) # approximately 0.69

EDIT

The asymmetric Laplace distribution is an example where the distribution extends over the entire real line, not just the positive numbers. (In more technical language, the PDF has support on all of $\mathbb R$.)

Max
  • 139
  • 5
Dave
  • 28,473
  • 4
  • 52
  • 104
13

The mean is the point where the area left and right between the CDF and the vertical line through the mean are equal.

For symmetric distributions, the left and the right side/area have the same shape and you get that the mean is at the point where the CDF is equal to 0.5 (also the median).

For non-symmetric distributions the shapes are different, so this equality of area does not need to be true (obviously it can be equal, but it does not need to be equal).

For any distribution where the mean and median is different, you have that the CDF of the mean is not 0.5.

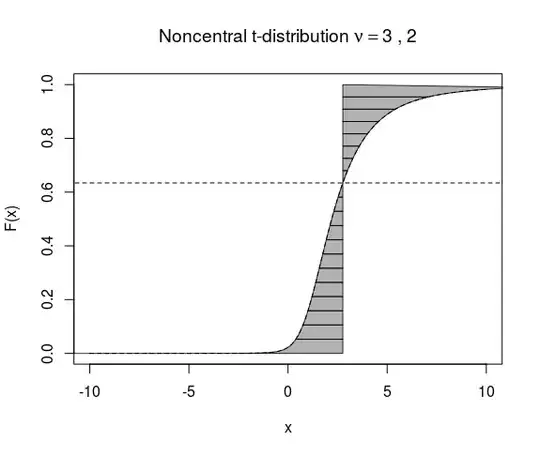
An example is a non-central t-distribution which is plotted below.

example

Sextus Empiricus
  • 43,080
  • 1
  • 72
  • 161
  • 1
    So, if $\mu = E[X]$ and $F$ is continuous, we have $\int_{-\infty}^\mu F(t)dt = \int_{\mu}^\infty (1-F(t))dt$?. Do you have a quick reference? I do not remember this result. – Lucas Prates Jan 19 '22 at 12:01
  • 2
    I do not know a direct statement of $\int_{-\infty}^\mu F(t)dt = \int_{\mu}^\infty (1-F(t))dt$ I view it intuitively as integrating the quantile function $E[X] = \int_0^1 Q_X(p) dp$ or [this expression](https://en.wikipedia.org/wiki/Expected_value#General_case) – Sextus Empiricus Jan 19 '22 at 12:06
  • 3
    It follows from$$\int_{-\infty}^\mu F(t)\text dt=\mu F(\mu)-\int_{-\infty}^\mu t \text dF(t)$$and$$\int^{\infty}_\mu (1-F(t))\text dt=-\mu +\mu F(\mu)+\int^{\infty}_\mu t \text dF(t)=\mu F(\mu)-\int_{-\infty}^\mu t \text dF(t)$$ – Xi'an Jan 19 '22 at 12:08
  • Here is a related form https://en.wikipedia.org/wiki/Expected_value#Basic_properties $$E[X] = \int_0^{\infty} 1-F(x) dx - \int_{-\infty}^0 F(x) dx $$ – Sextus Empiricus Jan 19 '22 at 12:11
  • @Sextus Empiricus I see that it can be seen as integrating the quantile function, but it is not intuitive (yet) why the areas should be equal if I we chose to "split" at the expected value. – Lucas Prates Jan 19 '22 at 12:26
  • 1
    @Xi'an very clean, thank you! – Lucas Prates Jan 19 '22 at 12:27
  • @SextusEmpiricus yes, that property implies the result when $E[X] = 0$, but is not direct when it is not $0$. – Lucas Prates Jan 19 '22 at 12:27
  • 1
    @Lucas We have $$E[X] = \int_0^1 Q_X(p) dp$$ and we can change this like the following which is considering the integral of the quantile function with a shift, which is like the area between $F(x)$ and the vertical line through $E[X]$ $$0 = \int_0^1 Q_X(p)-E[X] dp$$ or $$ \underbrace{\int_0^m Q_X(p)-E[X] dp}_{\text{negative of area leftside}} + \underbrace{\int_m^1 Q_X(p)-E[X] dp}_{area rightside}$$ where $m$ is the quantile of the expectation value. – Sextus Empiricus Jan 19 '22 at 12:29
  • Apologies if this is just a translation error on my side, but shouldn't the phrase "For asymmetric distributions, the left and the right side/area have the same shape" start with "For symmetric..."? – nope Jan 19 '22 at 12:38
  • @SextusEmpiricus I see it now! This is an interesting show to prove the result, thank you for the detailed explanation. – Lucas Prates Jan 19 '22 at 12:42
  • @Xi'an I didn't mean to say that asymetric distribution *need* to have a different mean and median. Did it come across like that too much? – Sextus Empiricus Jan 19 '22 at 16:40
8

As others have said, no. In fact, it can be any number in $(0, 1$).

Let $\epsilon \, \in \, (0,1)$, consider the random variable $X$ such that $\mathbb{P}(X = -1) = \epsilon$ and $\mathbb{P}(X = \frac{\epsilon}{1-\epsilon}) = 1 - \epsilon$. The mean is

$$E[X] = -\epsilon + (1-\epsilon)\frac{\epsilon}{1-\epsilon} = 0 \quad, $$

and $F(0) = \epsilon$.

As observed in the comments, $1$ can also be attained by the CDF if we consider a constant random variable.

Lucas Prates
  • 1,183
  • 4
  • 15
  • 2
    The point 1 is also included if you consider [degenerate distributions](https://en.wikipedia.org/wiki/Degenerate_distribution) (eg. constants). – Sextus Empiricus Jan 19 '22 at 11:17
5

No.

A counterexample will be $X \sim Exp(1)$. The mean of $X$ is 1, and $P(X < 1)$ is $1 - 1/e$, around 0.63.

B.Liu
  • 1,025
  • 5
  • 17