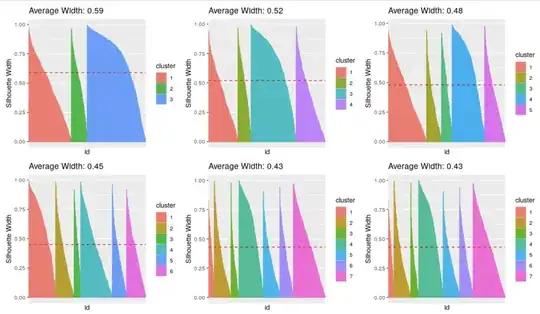
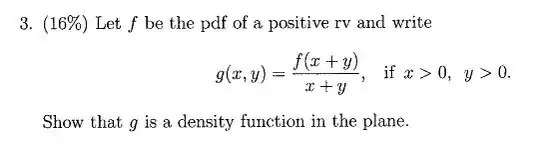I have a practical question. I am trying to select the number of clusters in k-means clustering and I have tried a Silhouette analysis, an elbow plot looking at the residuals, and a hierarchical clustering. However I still cannot decide how many clusters to pick since it is not that straightforward in my case. For my research (to avoid Reviewer 2 angry) I should be able to justify the number of k clusters. Based on these plots, I would really appreciate if anyone could give me some insight.
EDIT
My data is 2-dimensional, I have irregulary-unevenly spaced measurements of glucose in blood, for many patients. Then, I want to find if there are groups of patients whose progression of glucose looks differently. The objective is to understand the characteristics of each group in order to (hopefully) find interesting associations e.g. patients with kidney failure tend to have higher glucose levels sooner. For this purpose I use an EM algorithm which uses thin-plate splines and k-means. I am using a very similar approach to this one: https://cran.r-project.org/web/packages/clustra/vignettes/clustra_vignette.html