The question "What's the idea behind how more players means smoother?" invites us to explore the visual impression of smoothness of histograms obtained from larger and larger samples of a distribution that has a smooth density function.
Histograms
To study the situation, suppose we fix a set of bins delimited by cutpoints once and for all, so that we aren't confused by the effects of changing bin widths. What this means is we will partition the real numbers according to a finite sequence of distinct values
$$-\infty = c_{-1} \lt c_0 \lt c_1 \lt \cdots \lt c_{b} \lt c_{b+1}=\infty$$
(the cutpoints) and, for any index $i$ from $0$ through $b+1,$ define bin $i$ to be the interval $(c_{i-1}, c_i].$ Bins $0$ and $b+1$ are infinite in extent and the others have finite widths $h_i = c_{i} - c_{i-1}.$
Given any dataset of numbers $(x_1, x_2, \ldots, x_n),$ all of which lie in the interval $(c_1, c_b]$ covered by the finite-width bins, we may construct a histogram to depict the relative frequencies of these numbers. The bin counts
$$k_i = \#\{x_i\mid c_{i-1}\lt x_i \le c_i\}$$
are expressed as proportions $k_i/n$ and then converted to densities per unit length $q_i = (k_i/n) / h_i$ and plotted as a bar chart. Thus, the bar erected over the interval $(c_{i-1}, c_i]$ has height $q_i,$ width $h_i,$ and consequently has an area of $q_i h_i = k_i/n.$ Histograms use area to depict proportions.
Notice that the sum of the areas in a histogram is $k_1/n + k_2/n + \cdots + k_b/n = n/n = 1.$
Histogram of Random Samples
Let the fixed underlying distribution be a continuous one with a piecewise continuous density function $f.$ Suppose the numbers $(x_1, \ldots, x_n)$ are a random sample from this distribution (restricted, if necessary, to those values lying within the finite portion of the histogram from $c_0$ through $c_b$). By definition of $f,$ the chance that any particular random value $X$ drawn from this distribution lies in bin $i$ is
$$\Pr(X \in (c_{i-1}, c_i]) = \int_{c_{i-1}}^{c_i} f(x)\,\mathrm{d}x.\tag{*}$$
Let's call this probability $p_i.$ The indicator that $X$ lies in bin $i$ therefore is a Bernoulli random variable with parameter $p_i.$ Consequently,
In a random sample of size $n,$ the distribution of the bin count $k_i$ in bin $i$ is Binomial$(n, p_i).$
Since the variance of such a distribution is $n(p_i)(1-p_i),$ the variance of the histogram bar height is
$$\operatorname{Var}(q_i;n) = \operatorname{Var}\left(\frac{k_i}{nh_i}\right) = \frac{p_i(1-p_i)}{n\,h_i^2}.$$
Consequently, as $n$ grows large the variance of any of the histogram bars shrinks to its expected value $p_i$ in inverse proportion to $n.$ The result is a discrete approximation to $f:$ it is the ideal to which the histograms will approach as the sample size grows large.
These plots show, from left to right, (1) a histogram of a sample of size $n=100$ from a standard Normal distribution, constructed with cutpoints at $-4, -1.67, -1.48, ..., 4;$ (2) a histogram of a separate sample of size $n=1000;$ (3) the discretized density values $p_i$ given by formula $(*);$ and (4) a graph of the density function $f$ itself (which is also shown lightly in (3) for reference).
Smoothness of Histograms
Visual smoothness, then, depends on two aspects of the situation: the positions of the cutpoints and the (mathematical) smoothness of $f.$ The figure is typical: $f$ is a piecewise continuous function and enough cutpoints have been chosen, at a suitably tight spacing, to create a relatively gradual and regular "stairstep" appearance in the discretized version of $f.$ In particular, except at the mode of $f,$ there are no spikes in the bars.
Contrast this with the appearance of the left histogram in the figure, in which I count seven spikes (near $-1.7, -1, -0.3, 0.3, 0.8,$ $1.2,$ and $1.7$) with six dips between them. In the second histogram for a larger sample, there are two spikes on either side of $0$ with a tiny dip between them, but otherwise all the graduations follow the idealized pattern of the discretized density function.
The chances of such extraneous random spikes and dips decrease to zero as $n$ grows large.
This is straightforward to show. Here is some intuition. Consider a sequence of three consecutive bins indexed by $i,i+1,$ and $i+2,$ with corresponding densities $q_i,$ $q_{i+1},$ and $q_{i+2}.$ Their bars form a "stairstep" in the histogram whenever $q_{i+1}$ falls strictly between its neighboring values. The histogram of a random sample, on the other hand, will have random heights of $k_i / (n h_i).$ They will form a spike or a dip only when the middle random height is either the largest of the three or the smallest of the three. As $n$ grows large, (a) these heights vary less and less around their expected values $q_{*}$ and (b) although the heights are correlated (a spike somewhere in the histogram has to be compensated by a general lowering of all other bars to keep their total area equal to $1$), this correlation is small, especially when all the $p_i$ are smal, as in any detailed histogram. Consequently, for large $n,$ it is ever less likely that random fluctuations in the middle count $k_{i+1}$ will cause the histogram to spike or dip at that location.
Analysis with a Random Walk
That was a hand-waving argument. To make it rigorous, and to obtain quantitative information about how the chances of spikes or dips depend on sample size, fix a sequence of three consecutive bins $i,i+1,i+2.$ Collect a random sample and keep track of all bin counts as you do so. The cumulative counts $(X_n,Y_n)=(k_i-k_{i+1},k_{i+2}-k_{i+1})$ for sample sizes $n=1,2,3,\ldots$ define a random walk in the (integral) plane beginning at its origin. There are four possible transitions depending on which bin the new random value falls in, according to this table:
$$\begin{array} \text{Bin} & B_X & B_Y & \text{Probability} \\
\hline
i & 1 & 0 & p_i\\
i+1 & -1 & -1 & p_{i+1}\\
i+2 & 0 & 1 & p_{i+2}\\
\text{Any other} & 0 & 0 & 1 - (p_i+p_{i+1}+p_{i+2})
\end{array}
$$
$B_X$ and $B_Y$ denote the increments to $(X_n,Y_n),$ thereby forming a sequence of independent increments $(B_{X1},B_{X2}), \ldots, (B_{Xn},B_{Yn})$ whose partial sums form the random walk: $X_n = B_{X1} + \cdots + B_{Xn}$ and likewise for $Y_n.$
The histogram after $n$ steps will have a spike or dip at bin $i+1$ if and only if this walk ends up either with both differences negative or both differences positive: that is, $(X_n,Y_n)$ is in the interior of the first or third quadrants.
From the table, using the elementary definitions of expectation and covariance, compute that
$$E[(B_X,B_Y)] = (p_i-p_{i+1}, p_{i+2}-p_{i+1})$$
and
$$\operatorname{Cov}(B_X,B_Y) = \pmatrix{p_i+p_{i+1}-\left(p_i-p_{i+1}\right)^2 & p_{i+1} - \left(p_i-p_{i+1}\right)\left(p_{i+2}-p_{i+1}\right) \\
p_{i+1} - \left(p_i-p_{i+1}\right)\left(p_{i+2}-p_{i+1}\right) & p_{i+2}+p_{i+1}-\left(p_{i+2}-p_{i+1}\right)^2}.$$
The multivariate Central Limit Theorem tells us that for sufficiently large $n,$ $(X_n,Y_n)$ will have an approximately Binormal distribution with parameters $\mu_n=nE[(B_X,B_Y)]$ and $\Sigma_n=n\operatorname{Cov}(B_X,B_Y).$ When the ideal discretized version of the density has no spike or dip, $p_{i+1}$ lies between $p_i$ and $p_{i+2}.$ This places $\mu_n$ squarely within the first or third quadrant and makes it vanishingly unlikely that $(X_n,Y_n)$ will be anywhere else, QED.
Example: Histograms of Samples of Uniform Distributions
Finally, it is amusing that when the density is flat at bin $i+1$ (all three probabilities are equal), the covariance is a multiple of $\pmatrix{2&1\\1&2}$ while the expectation is the origin $\mu=(0,0).$ We easily compute that the limiting chance of a spike or dip is $2/3$ (spikes have a $1/3$ chance and dips have the same chance). This is what we would expect to see in a histogram of a uniform distribution on an interval, for instance (except at the two bars at either end). Thus, on average, two-thirds of the bars in a detailed histogram of a large uniform sample will be spikes or dips.
This is R code to simulate large uniform samples, count their spikes and dips, and compare the mean counts with these asymptotic expectations.
nspikes <- function(k) { # Counts the spikes in an array of counts
n <- length(k); sum(k[-c(1,n)] > pmax(k[-c(n, n-1)], k[-c(1,2)]))
}
b <- 32 # Number of bins
sim <- replicate(1e2, {
k <- tabulate(ceiling(runif(1e5, 0, b)), nbins=b)
c(Spikes=nspikes(k), Dips=nspikes(-k))
})
rbind(Expected=c(Spikes=(b-2)/3, Dips=(b-2)/3), Observed=rowMeans(sim))
Here is an example of its output (with histograms of 32 bins):
Spikes Dips
Expected 10.00 10.00
Observed 9.78 9.77
Here is the upper tip of the histogram of the first sample in this simulation, with spikes (red) and dips (blue) marked:
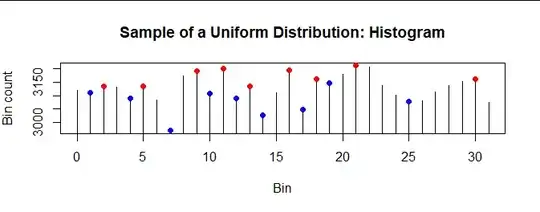
(To make the patterns clear, I have replaced each bar in this histogram by a vertical line through its center and do not use zero as the origin.) This particular histogram has nine spikes and nine dips, each comprising 30% of the 32-2 = 30 interior bins: both numbers are close to the expected $1/3$ proportion.