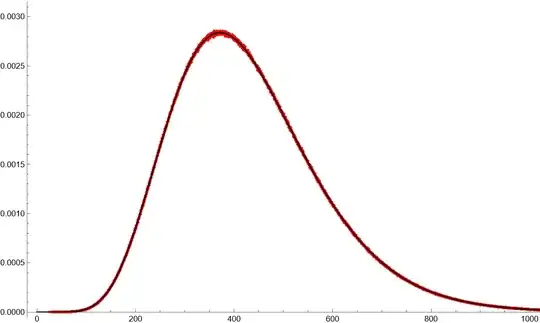
Let $Y=X^4$ where $X \sim N(u,\sigma^2)$ so:
$G_{Y}(y)=P(Y\leq y)$
$G_{Y}(y)=P(X^4\leq y)
\\
\\
G_{Y}(y)=P(\sqrt X^4\leq \sqrt{y})
\\
\\
G_{Y}(y)=P(|X^2|\leq \sqrt{y})
\\
\\
G_{Y}(y)=P(X^2\leq \sqrt{y})
\\
\\
G_{Y}(y)=P(|X|\leq y^{1/4})
\\
\\
G_{Y}(y)=P(- y^{1/4}\leq X\leq y^{1/4})
\\
\\
G_{Y}(y)=G_{X}(y^{1/4})-G_{X}(-y^{1/4})
$
Where $G_{X}$ is the cumulative of $X$, remember that $Y$ distribution can be get as $f_{Y}(y)=G_{Y}^{'}(y)$ then:
$f_{Y}(y)=4y^{-3/4}f_{X}(y^{1/4})+4y^{-3/4}f_{X}(-y^{1/4})$
where $f_X(.)$ is the $X$ distribution applied to $(.)$
Now we are seeking for its support:
As $x^4$ is a non negative function so its minimal is equal to $0$ and its maximum is $\infty$ so $Y$ support is given by:
$A_Y=(0,\infty)$