In short: 1 Roughly speaking you can see the distribution of $O_i - E_i$ as independent from the distribution of $E_i$. So if $E_i$ is a lot different from the true value does not matter so much for $O_i - E_i$. 2 The role of the $E_i$ in the denominator will be small if the observed numbers are sufficiently high.
Lets for simplicity consider the case where we only have 2 categories
$$\begin{array}{c|cc}
& \text{category 1} & \text{category 2} \\
\hline
\text{variable 1} &O_{11} & O_{12} \\
\text{variable 2}& O_{21} & O_{22} \\
\end{array} $$
and we fix the number of observations to $n$. Then due to the dependency we have basically only two observations. This simplifies the case because we can view it 2d and plot it.
$$\begin{array}{c|cc}
& \text{category 1} & \text{category 2} \\
\hline
\text{variable 1} &x & n-x \\
\text{variable 2}& y & n-y \\
\end{array}$$
Let's consider $n = 100$ and the hypothetical true categorical distribution has a fifty-fifty distribution for both categories.
Then $x$ and $y$ (and the related $O_{ij}$) will be binomially distributed, but they can also be approximated as a normal distribution. Below a distribution is sketched by showing a sample of 1000 points
In the image, we also show how we can intuitively view the computation of the $\chi^2$ statistic. It can be based on the residual vector of the model which projects the observation $x,y$ onto the point $\beta,\beta$, on the diagonal line (with $\beta = (x+y)/2$). Where the length of this line is
$$d = \sqrt{\left( x-\beta \right)^2 + \left( y-\beta \right)^2 }$$
and $\beta$ is
$$\beta = \frac{x+y}{2}$$
We can relate this $\beta$ and $d$ to the following
approximately normal and independent distributed variables with
$$\begin{array}{}
d & \sim & N(\mu = 0,&\sigma^2 = 0.5 n) \\
\beta & \sim & N(\mu = n/2,& \sigma^2 = 0.5 n)
\end{array}$$
the $\chi^2$ statistics equal to:
$$\begin{array}{}
\chi^2 &=& \frac{(O_{11}-E_{11})^2}{E_{11}} + \frac{(O_{12}-E_{12})^2}{E_{12}} + \frac{(O_{21}-E_{21})^2}{E_{21}} + \frac{(O_{22}-E_{22})^2}{E_{22}} \\
&=& \frac{(x-\beta)^2}{\beta} + \frac{(y-\beta)^2}{n-\beta} + \frac{(x-\beta)^2}{\beta} + \frac{(y-\beta)^2}{n-\beta} \\
&=& \frac{\frac{1}{2} d^2}{\beta} + \frac{\frac{1}{2} d^2}{n-\beta} + \frac{\frac{1}{2} d^2}{\beta} + \frac{\frac{1}{2} d^2}{n-\beta} \qquad \text{using $\beta^\prime = \beta-0.5n$} \\
&= &\frac{d^2}{(0.5n-\beta^\prime)(0.5n+\beta^\prime)} \\
& \approx& \frac{d^2}{(0.5 n)^2}
\end{array}$$
What if $E_i$ happens to be far from the true expected value?
So in the view of the $\chi^2$ statistic approaching the chi-squared distribution as the above-explained approximation we see the influence of $E_i$ disappear in two points.
- The error terms in the numerator $(O_i - E_i)^2$ are like the residuals, and independently$^1$ distributed from the estimate $E_i$.
- The expression of $E_i$ in the denominator has only a very small influence if the numbers are high. The numbers $E_i$ may already have a small coefficient of determination (if the numbers are high), but also the increase of one $E_i$ is paired with the decrease of another $E_i$, and this dampens the effect on the chi-squared statistic even more.
1) an example/illustration of this independence is made with the following image and R-code
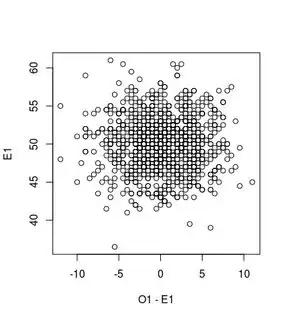
set.seed(1)
O1 = rbinom(n,100,0.5)
O2 = rbinom(n,100,0.5)
E1 = 0.5*(O1+O2)
plot(O1-E1, E1)

