I'm working on an implementation of PCA that works on very large data sets.
Based on my understanding of the algorithm, the first step is to do an SVD of the input m x n matrix, X. This SVD looks like X = WΣVT. The "interesting" output Y of this process -- from Wikipedia, "The PCA transformation that preserves dimensionality (that is, gives the same number of principal components as original variables)" -- is given by the following equation:
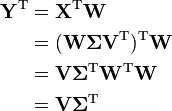
Based on my reading, if I can compute the W component of the SVD, then I can compute Y as:
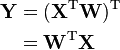
The upshot here is that I'd only have to compute W. In terms of computational and memory complexity, this approach is significantly more efficient because the only matrix above and beyond the initial data set I'd have to load has size m x m, which (at least in my case) is much smaller than V, which would be n x n.
Is there some reason why this derivation won't work that I'm not seeing?