I am playing around with GARCH models for the first time (I have a stats background but basically no experience with GARCH), trying to forecast volatility in a financial time series.
I trained a GARCH(1,1) model on 3,000 data points and forecasted 1 period ahead 500 times (retraining to include new data point after each prediction is made). Below are my results (the points/circles is the original time series, the line is the GARCH volatility prediction for that timepoint).
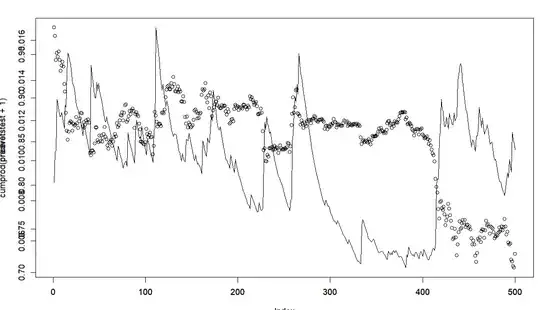
Please correct me if I'm wrong, but it seems that the GARCH model offers no predictive value. The "predicted" volatility values spike up after a big price move. I feel like these results could be replicated by just taking a rolling window of realized past volatility (as the GARCH model appears lagging, not predictive).
Does this seem wrong, or is this what results usually look like? Has anyone had any success with something like this? Any advice for what I might be doing wrong?
I have tried specifying the mean model as ARMA(0,0) and ARMA(1,1), no significant difference.
EDIT: I am adding my code to better supplement my question. To be clear, my data is NOT time bars, but volume bars (price sampled every time a certain threshold of volume is traded) as they have been shown to have better statistical properties. These volume bars are sampled, on average, every 4 hours (though changes significantly based on the level of trading activity).
library(rugarch)
library(forecast)
volumebardata <- read.csv(file='MyCSVFile', header=TRUE)
returns <- function(vector){
rets <- c()
for (i in 2:length(vector)){
rets <- c(rets, vector[i]/vector[i-1])
}
return(rets)
}
pricereturns <- (returns(volumebardata$VolumeBarClose))-1
priceretstrain <- pricereturns[1:3000]
priceretstest <- pricereturns[3001:3500]
# Specify a standard GARCH model with constant mean
garchspec <- ugarchspec(mean.model = list(armaOrder = c(0,0)),
variance.model = list(model = "eGARCH",
garchOrder=c(1,1),
variance.targeting=FALSE),
distribution.model = "std")
# Estimate the model
garchfit <- ugarchfit(data = priceretstrain, spec = garchspec)
predvol <- c()
for (i in 1:300){
if (i > 1){
# Specify a standard GARCH model with constant mean
garchspec <- ugarchspec(mean.model = list(armaOrder = c(0,0)),
variance.model = list(model = "eGARCH",
garchOrder=c(1,1),
variance.targeting=FALSE),
distribution.model = "std")
# Estimate the model
fulldata <- c(priceretstrain, priceretstest[1:(i-1)])
garchfit <- ugarchfit(data = fulldata, spec = garchspec)
}
# Forecast volatility 1 period ahead
garchforecast <- ugarchforecast(fitORspec = garchfit,
n.ahead = 1)
# Extract the predicted volatilities and print them
predvol <- c(predvol, sigma(garchforecast))
}
plot(cumprod(priceretstest+1)[1:500], type='l')
par(new=TRUE)
plot(predvol[1:500], type='l')
Additionally, here is a zoomed in plot of the GARCH-predicted volatility (red line) vs. the squared returns (as proxy for "true" volatility, shown in black). You can quite clearly see the time-lag.
EDIT 2: Several commenters are pointing out that I might be measuring volatility incorrectly, therefore of course the GARCH predictions appear incorrect. However, I don't understand why the model is being defended when clearly the volatility predictions lag behind the actual rapid shifts in the time series (regardless of how you measure it), making the predictions obviously useless because I can derive the same kind of predictions with a V(t+1)=V(t) "prediction" model. Am I misusing GARCH? Or is it just not all that great of a volatility prediction model?