Let's solve this in all dimensions $d=1,2,3,\ldots.$
The (vector) increments of the walk are $\mathbf{X}_i = (x_{1i}, x_{2i}, \ldots, x_{di}).$ After $n$ such independent steps the walk has reached the point $\mathbf{S}_n = \mathbf{X}_1 + \mathbf{X}_2 + \cdots + \mathbf{X}_n$ with corresponding components $s_{1n}, \ldots, s_{dn}.$ The question asks for the expectation of $|\mathbf{S}_n| = \sqrt{s_{1n}^2 + \cdots + s_{dn}^2}$ for large $n.$
Because the $\mathbf{X}_i$ are uniformly distributed on the unit sphere,
Their components are identically distributed. (Thus, in particular, they have identical means, variances, and covariances. Details are given at https://stats.stackexchange.com/a/85977/919, but this additional information is not necessary for the following analysis.)
Their means are all zero (since the spherical symmetry implies the means equal their own negatives and the boundedness of the vectors implies the means exist and are finite.)
The variances of each $x_{ki}$ are all $1/d,$ because for any fixed $i,$ the sum of the variances of the $x_{ki}$ is the expectation of the sum of their squares, which is constantly $x_{1i}^2 + \cdots + x_{di}^2 = 1.$
Their covariances are all zero. This is a bit of a surprise, because the sum-to-square restriction implies the components of any $\mathbf{X}_i$ are not independent. Nevertheless, the spherical symmetry of the distribution of $\mathbf{X}_i$ implies the distribution of $y_i=(x_{1i} + x_{2i} + \cdots + x_{di})/\sqrt{d}$ is identical to that of any of the components, whence
$$\frac{1}{d} = \operatorname{Var}\left(y_i\right) = \frac{1}{d}\sum_{j,k=1}^d E\left[x_{ji}x_{ki}\right] = \frac{1}{d}\left(d\operatorname{Var}(x_{1i}) + d(d-1)\operatorname{Cov}(x_{1i}, x_{2i})\right).$$
Upon plugging in $1/d$ for the variance term on the right, we see the last term $d(d-1)\operatorname{Cov}(x_{1i},x_{2i})$ must be zero. Since either there is no covariance (for $d=1$) or else $d\gt 1,$ the covariance is zero, QED.
Because the increments are independent, the multivariate Central Limit Theorem (CLT) tells us the distribution of $\mathbf{S}_n$ is approximately multivariate Normal. The approximating Normal distribution's parameters are determined by the means and variances of the $\mathbf{X}_i:$ it will have zero mean, variances of $n/d,$ and zero covariances. Ergo,
the variables $(d/n)s_{kn}^2$ must be distributed approximately like squares of standard Normal variates and (therefore) their sum $(d/n)|\mathbf{S}_n|^2$ must be distributed approximately like the sum of squares of $d$ uncorrelated (whence independent) standard Normal variates.
By definition, a sum of independent standard Normal variables has a chi-squared distribution with $d$ degrees of freedom. Also by definition, its square root has a chi distribution with $d$ d.f. Its expectation is
$$ E\left[|\mathbf{S}_n|\right] = \sqrt{\frac{n}{d}}E\left[\sqrt{(d/n)s_{1n}^2 + (d/n)s_{2n}^2 + \cdots + (d/n)s_{dn}^2}\right] = \frac{\sqrt{2n}\,\Gamma((d+1)/2)}{\sqrt{d}\,\Gamma(d/2)}.$$
As a special case, when $d=2$ the right hand side is
$$\frac{\sqrt{2n}\,\Gamma((2+1)/2)}{\sqrt{2}\,\Gamma(2/2)} = \frac{\sqrt{n\pi}}{2},$$
exactly as noted in a comment to the question. When $d=3$ (the case of the question), the right hand side is
$$\frac{\sqrt{2n}\,\Gamma((3+1)/2)}{\sqrt{3}\,\Gamma(3/2)} = \frac{2\sqrt{2n}}{\sqrt{3\pi}}.$$
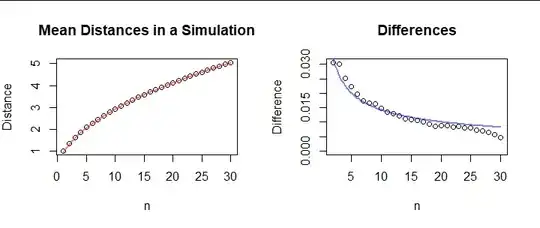
To illustrate the general formula, here is a plot of $\sqrt{2n}\,\Gamma((d+1)/2) / (\sqrt{d}\,\Gamma(d/2))$ for $d=3$ (in red) along with the means of 1,000,000 simulated random walks at times $1$ through $n=30.$ They look to be in good agreement, especially for $n\gt 1.$ The differences between the means and this formula approach zero at a rate of $O(n^{-1/2})$ (plotted in blue) or better, as predicted by the CLT.