2

This question follows closely this paper .

I'm trying to fully understand how Ordered Target Statistics (TS) (for CatBoost) works. E.g. the CatBoost algorithm uses this method to group categorical features through estimatation of numerical values $\hat{x}_{k}^{i} \approx \mathbb{E}\left(y \mid x^{i}=x_{k}^{i}\right)$ instead of one-hot-encode them.

Since this estimate can be noisy for low-frequency categories, one can smooth it by some prior p so that :

$\hat{x}_{k}^{i}=\frac{\sum_{j=1}^{n} \mathbb{1}_{\left\{x_{j}^{i}=x_{k}^{i}\right\}} \cdot y_{j}+a p}{\sum_{j=1}^{n} \mathbb{1}_{\left\{x_{j}^{i}=x_{k}^{i}\right\}}+a}$ where $a>0$ is some parameter.

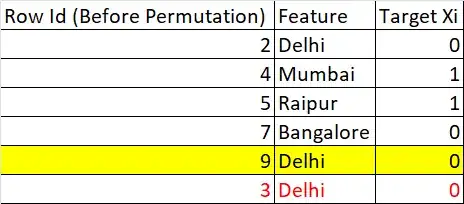
Now, one uses the ordering principle which translates to me to order the (whole) data set $\mathcal{D}$ or some subsets of the dataset $\mathcal{D}_k$ given some ordering function. I anticipate that the ordering function in the CatBoost algorithm is the artificial "time" which they define as a random permutation $\sigma$ of the training examples. Then, for each example they use all the available "history".

What is meant by "history" in this method?

My best guess would be the following. In each step a random permutation is applied to $\mathcal{D}$. Afterwards $\mathcal{D}$ is split into training and test examples. Then the test examples were expanded with all the training examples of the past steps.

mugdi
  • 176
  • 1
  • 7

1 Answers1

1

Catboost in order to calculate the ordered target statistics defines various permutations of the training data. Now at each step of the gradient boosting it chooses one of the permutation at random in order to calculate ordered ts.

Now the history refers the sample that appears before. Now lets look at the random sample from permutation below:

enter image description here

for Row ID - 9 , history comprises of Row ID - 2 but not Row ID - 3 as in this permutation it occurs after Row ID - 9

Ashwiniku918
  • 131
  • 1