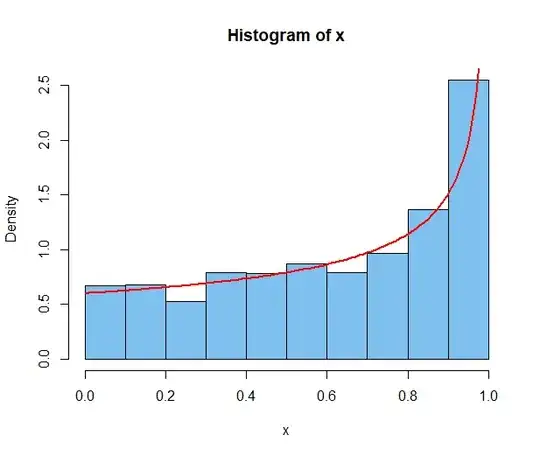
Let us consider the histogram of a random variable. It is uniform up to a certain value $\bar{x}$, while beyond it a growth is present,as shown in the figure. I would like to obtain an estimate of the value of $\bar{x} \pm \sigma_x$ with an associated error, without making any assumptions on the shape of growth for $X>\bar{x}$, i.e. without assuming that it is linear, exponential etc. Making the assumption I think one could proceed performing a fit (non-linear least squares) and get the desired point with its own uncertainty.
Asked
Active
Viewed 25 times
0
-
1Least squares usually is not an appropriate way to fit distributions. Could you explain *why* you are trying to do this and how you would interpret $\bar x$? – whuber Dec 29 '21 at 23:28
-
Histograms are sensitive to the cell border position. Have you tried a kernel density estimate? Then you can look for the "elbow" (point of highest curvature) in the density. – cdalitz Dec 30 '21 at 06:45
-
If you are wedded to the use of least-squares approaches, then at least consider basing the analysis on the rootogram version of the histogram (as illustrated at https://stats.stackexchange.com/a/424979/919, for instance). Then at least the errors are nearly homoscedastic. It would be plausible to apply a suitable [changepoint procedure](https://stats.stackexchange.com/questions/tagged/change-point) to that, perhaps supplemented with a sensitivity analysis of the choices of bin cutpoints. – whuber Dec 30 '21 at 19:02
1 Answers
0
As always, it would be a good idea to answer our moderator, @whuber's questions. Also, it might help to show numbers along both axes of your plot.
Pending those modifications of your question, I'll speculate that your histogram might show a sample from a beta population. In the R code below a random sample of size $n=1000$ from the population $\mathsf{Beta}(1,.6)$ is used:
set.seed(1220)
x = rbeta(1000, 1, .6)
hist(x, prob=T, col="skyblue2")
curve(dbeta(x,1,.6), add=T, lwd=2, col="red")
BruceET
- 47,896
- 2
- 28
- 76