- Why do we need the conditional distribution and how we interpret the result?
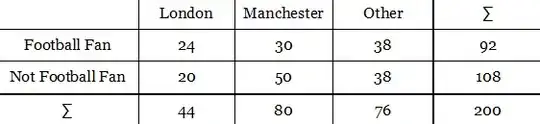
In your data, you can calculate the probability for the Manchester subgroup of belonging to the group "Football Fan" as 30/(30+50)=0.37, while the probability for other cities may differ, for example it is 24/(20+24)=0.54 for London, or 92/(92+108)=0.46 for all the data. Those are empirical probabilities, the estimates of the probabilities from your sample.
- Is conditional distribution different from conditional probability distribution?
In probability theory, we are dealing with probability distributions. If you are referring to the empirical (observed) distribution of the data, it can be presented as counts $n_i$ (frequency distribution) or empirical probabilities $n_i \big/ \sum_i n_i$ (probability distribution).