Can someone please explain what type of vcov (standard errors) argument is best for the following model:
$Y_{g,t, i} = \alpha + \beta Treat_g + \delta (Treat_g \times After_t) + \gamma Month + u_{g,t}$
where $Treat$ equals 1 for the treatment group, 0 otherwise. The DiD-estimator $Treat \times After$ equals 1 in the post-treatment period, 0 otherwise. And finally, $Month$ is a set of 15 dummies (I believe time-effects is the correct term, but I am not sure).
The dependent variable is employment. Note that I actually have 12 different models with 12 different dependent variables. Each model contains different income quartiles or workers in different sectors.
My question to you is, how do I correct the standard errors? I've tried a few, and they change the standard errors quite a bit. Just FYI, I use R to estimate these models.
Just two examples:
- Using "robust" gives me 3 out of 12 models with a significance of at least 95%
- If I use "HC2", I get 8 out of 12!
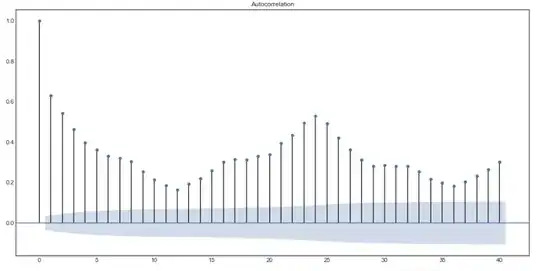
Here's a screenshot of (parts of) number 2:
Let me know if I can add or clarify something!
EDIT:
Another note. The data I have is on employment (among other things), from all US states. I have created a new database with only a treatment group and a control group, where the employment is the mean for each group. However, it is possible to keep the data as is and maybe cluster standard error on state -- if that is the better solution.