Histogram with uniform vs non-uniform Bins

Question

This question describes the basic difference between a uniform and a nonuniform histogram. And this question discusses the rule of thumb for picking the number of bins of a uniform histogram that optimizes (in some sense) the degree to which the histogram represents the distribution from which the data samples were drawn.

I can't seem to find the same kind of "optimality" discussion about uniform vs non-uniform histograms. I have a clustered nonparametric distribution with far away outliers so a non-uniform histogram intuitively makes more sense. But I would love to see a more precise analysis of the following two questions:

When is a uniform-bin histogram better than a non-uniform bin one?
What is a good number of bins for a non-uniform histogram?

For a non-uniform histogram, I am considered the simplest case where we take $n$ samples from an unknown distribution, order the resulting $n$ values, and separate them into $k$ bins such that each bin has $\frac{k}{n}$ of these samples (assuming that $n \equiv c k$ for some large integer $c$). The ranges are formed by taking the midpoint between the $\max$ of the values in bin $i$ and the $\min$ of the values in bin $i+1$. Here and here are links that describe these type of non-uniform histograms.

There's not nearly enough information to answer (2). What are the conditions on non-uniformity? Can you choose any bins you like, or is there some restriction? What do you want to optimize? e.g. do you want minimum mean integrated squared error between $f$ and $\hat{f}$? Or something else? — Glen_b, Apr 10 '13 at 23:31
@Glen_b I describe in a little more detail the kind of histogram I am considering in the non-uniform bin case. — Alan Turing, Apr 10 '13 at 23:43
Check your edit. Did you mean "n = cm" rather than "cn"? Also there's a later typo. — Glen_b, Apr 10 '13 at 23:47
Are you trying to convey something like [this](http://gallery.r-enthusiasts.com/graph/Histogram_with_equal_counts_89)? — Glen_b, Apr 10 '13 at 23:50
Also see [this discussion](http://stats.stackexchange.com/a/29107/805) of a compromise between that and the usual histogram — Glen_b, Apr 11 '13 at 00:00
@Glen_b, both the links you provide and the fixes you suggest are spot on. In fact the link to the discussion would make for a good answer. — Alan Turing, Apr 11 '13 at 01:59
Thanks. A rather different approach to the same problem occurred to me as well. I'll edit the whole thing into an answer shortly so it's all together. — Glen_b, Apr 11 '13 at 02:13

score 7 · Accepted Answer · edited Apr 13 '17 at 12:44

When is a uniform-bin histogram better than a non-uniform bin one?

This requires some kind of identification of what we'd seek to optimize; many people try to optimize average integrated mean square error, but in many cases I think that somewhat misses the point of doing a histogram; it often (to my eye) 'oversmooths'; for an exploratory tool like a histogram I can tolerate a good deal more roughness, since the roughness itself gives me a sense of the extent to which I should "smooth" by eye; I tend to at least double the usual number of bins from such rules, sometimes a good deal more. I tend to agree with Andrew Gelman on this; indeed if my interest was really getting a good AIMSE, I probably shouldn't be considering a histogram anyway.

So we need a criterion.

Let me start by discussing some of the options of non-equal area histograms:

There are some approaches that do more smoothing (fewer, wider bins) in areas of lower density and have narrower bins where the density is higher - such as "equal-area" or "equal count" histograms. Your edited question seems to consider the equal count possibility.

The histogram function in R's lattice package can produce approximately equal-area bars:

library("lattice")
histogram(islands^(1/3))  # equal width
histogram(islands^(1/3),breaks=NULL,equal.widths=FALSE)  # approx. equal area

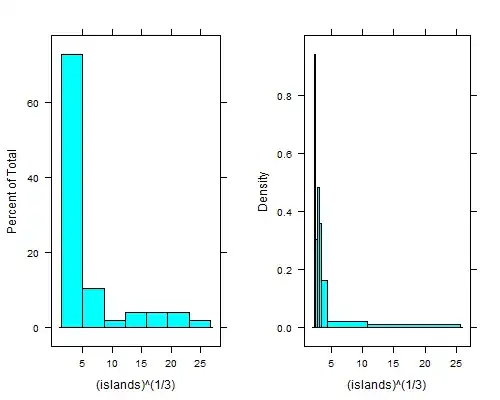
comparison of equal width and equal area

That dip just to the right of the leftmost bin is even clearer if you take fourth roots; with equal-width bins you can't see it unless you use 15 to 20 times as many bins, and then the right tail looks terrible.

There's an equal-count histogram here, with R-code, which uses sample-quantiles to find the breaks.

For example, on the same data as above, here's 6 bins with (hopefully) 8 observations each:

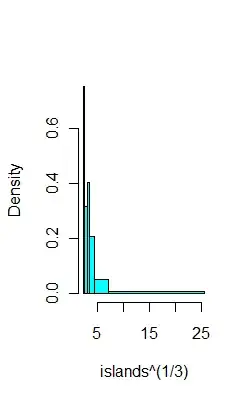
equalcount histogram

ibr=quantile(islands^(1/3),0:6/6)
hist(islands^(1/3),breaks=ibr,col=5,main="")

This CV question points to a paper by Denby and Mallows a version of which is downloadable from here which describes a compromise between equal-width bins and equal-area bins.

It also addresses the questions you had to some extent.

You could perhaps consider the problem as one of identifying the breaks in a piecewise-constant Poisson process. That would lead to work like this. There's also the related possibility of looking at clustering/classification type algorithms on (say) Poisson counts, some of which algorithms would yield a number of bins. Clustering has been used on 2D histograms (images, in effect) to identify regions that are relatively homogenous.

--

If we had an equal-count histogram, and some criterion to optimize we could then try a range of counts per bin and evaluate the criterion in some way. The Wand paper mentioned here [paper, or working paper pdf] and some of its references (e.g. to the Sheather et al papers for example) outline "plug in" bin width estimation based on kernel smoothing ideas to optimize AIMSE; broadly speaking that kind of approach should be adaptable to this situation, though I don't recall seeing it done.

Histogram with uniform vs non-uniform Bins

1 Answers1