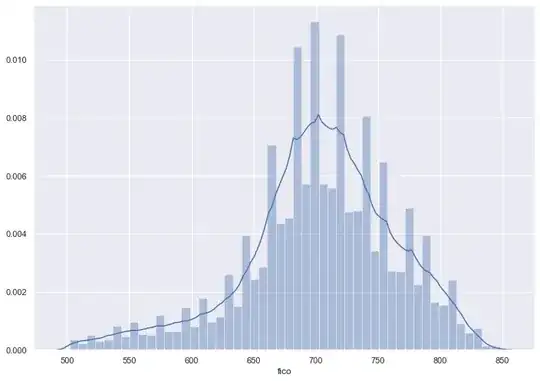
I am working on a binary classification problem where one of the most interesting features has a distribution which looks more or less bimodal. Here is the distribution plot of that feature:
The two modes seem to correspond to two classes. When I look at the distribution of this feature corresponding to each class separately, this is what I get:
Clearly, one of them is more like a log-normal distribution, and the other is more like normal, and the two peaks in the original distribution seems to correspond to two different classes. My question is how do I deal with this kind of bimodality in Logistic regression. Also, would other machine learning algorithms be more suitable for this kind of a problem?