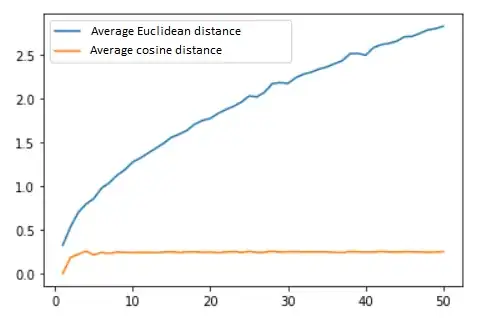
I've generated 100 random vectors (data points) in n∈[1,...,50] dimensions. I then compared distances between each pair of vectors and calculated the mean value. I've done this for all dimensions using Euclidean distance and then using cosine similarity.
Also worth noting is that all vectors are in range [0, 1)
This is the graph I get:
From what I've read on the topic, there shouldn't be a significant difference between these two measurements and both of them will be affected by the curse of the dimensionality.
AFAIK cosine similarity is only in the interval from [-1, 1] and in my case (all vectors are positive) the interval will be [0, 1]. Is that why the cosine similarity is "much" smaller than Euclidean distance? And also, how come the cosine similarity curve isn't rising with the number of dimensions?
Note: This is a question in my lab exercise: Which one of these measures would you use in high dimension space?
In my opinion there isn't a clear answer to this.