1

I found something intresting today!

I have always been doing PCA by using SVD with covariance when I want to reduce the dimension.

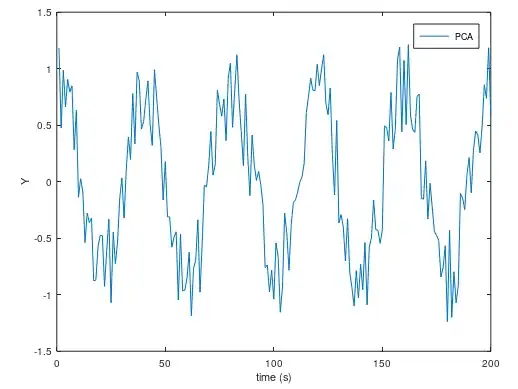
Assume that we have a vector $X = {x_0, x_1, x_2, \dots, x_n}$. $X$ contains lots of noise, but it's actually a sine curve. Let's remove that noise.

enter image description here

Covariance method:

  1. X = X - mean(X) % Center the data
  2. X = cov(X'*X); % Find covariance
  3. [U, S, V] = svd(X, 'econ'); % Use Singular value decompotision
  4. nx = 1; % Dimension
  5. X = U(:, 1:nx)*S(1:nx, 1:nx)*V(:, 1:nx)'; % Dimension reduce

When I plot $X$, I got this. The amplitude is better (it should be 1), but the noise is still there.

enter image description here

So I tried this instead.

  1. n = size(X, 2);
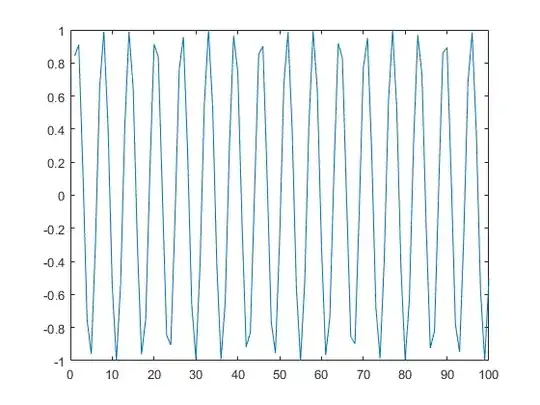
  2. H = hankel(X);
  3. H = H(1:n/2, 1:n/2); % Important with half hankel
  4. nx = 1; % Dimension
  5. [U, S, V] = svd(H, 'econ'); % Use Singular value decompotision
  6. X = U(:, 1:nx)*S(1:nx, 1:nx)*V(:, 1:nx)'; % Dimension reduce

And now I got this result. A much better result.

enter image description here

Question:

Is it better to use a hankel matrix instead of covariance matrix when reducing dimensions of data using PCA?

Nazi Bhattacharya
  • 203
  • 1
  • 8
  • Where do U, S and V come from when you're using the hankel function? – Sycorax Dec 08 '21 at 20:54
  • @Sycorax It's comming from dimension reduction for system identification. I tried to use that because system identification also using SVD. Look up Eigensystem Realization Theory. – Nazi Bhattacharya Dec 08 '21 at 21:15
  • 1
    No, I mean in your code. It looks like you skip the step where U, S and V are assigned. – Sycorax Dec 08 '21 at 21:31
  • @Sycorax Oh! Sorry. I missed the SVD. CTRL+C and CTRL+V slippering... – Nazi Bhattacharya Dec 08 '21 at 21:31
  • 2
    What covariance are you computing? You only have one variable – Firebug Dec 08 '21 at 21:33
  • @Firebug Well, in this case, I have only one variable. – Nazi Bhattacharya Dec 08 '21 at 21:33
  • I don't think `Sigma = cov(X'*X);` is what you mean to do. When $X$ is the centered data, then $X^\top X$ is proportional to the covariance. Computing the **covariance of** $X^\top X$ is something else. It's worthwhile to review the content at https://stats.stackexchange.com/questions/134282/relationship-between-svd-and-pca-how-to-use-svd-to-perform-pca I think you only need `svd(X)` to get the PC information you're after. – Sycorax Dec 08 '21 at 21:37
  • 1
    @Sycorax So in this case, I should not use `cov(X'*X)` function at all? Just use $svd(X)$ as I did with the hankel example? – Nazi Bhattacharya Dec 08 '21 at 21:42
  • 1
    Please review https://stats.stackexchange.com/questions/134282/relationship-between-svd-and-pca-how-to-use-svd-to-perform-pca for a complete explanation of how to use SVD to carry out PCA. But Firebug is correct -- you have 1 variable, so either method will only return .... 1 variable. Something else is going on, but I don't use this software... – Sycorax Dec 08 '21 at 21:43

0 Answers0