Intro to question
I am trying to understand sense of unbiasedness in hypothesis testing - here is the definition:
Consider a statistical hypothesis test of size level $0<\alpha<1$ for testing a null hypothesis $H_0:\theta \in \Theta_0 \subset \Theta$ against an alternative hypothesis $H_1:\theta \in \Theta_1=\Theta - \Theta_0$. The test is considered "unbiased" if its power function $\beta$ satisfies the condition:
$$\beta(\theta)\leq\alpha \hspace{0.3cm}\text{if}\hspace{0.3cm}\theta \in \Theta_0,$$ $$\beta(\theta)\geq\alpha \hspace{0.3cm}\text{if}\hspace{0.3cm}\theta \in \Theta_1.$$
Answer to this question: "Unbiased" hypothesis test --- what does it mean actually? provides an example of biased test:
Now, suppose you were to use that rule (reject if $t>1.645$) to test $\theta=0$ against $\theta\neq0$. The probability that the test will reject will decrease the more negative the true $\theta$, as we shall rarely observe large positive t-ratios in that case. In particular, this test is be biased, as $\beta(\theta)<\alpha$ when $\theta\in\Theta_1\cap(-\infty,0)$.
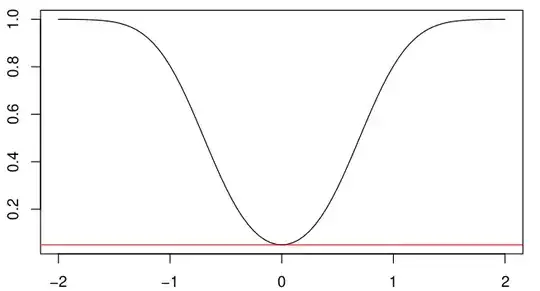
and graphical explanation which is a plot of power function for this particular test:

The question
In the comment someone asked what can we do about the fact that the test is biased. I think, that the solution is to use test statistic $|T|$ instead of $T$. Then power function will be symmetrical around $0$, something like this:
Can anyone confirm if it is true?