I'm trying to determine how well an observed distribution matches a theoretical one 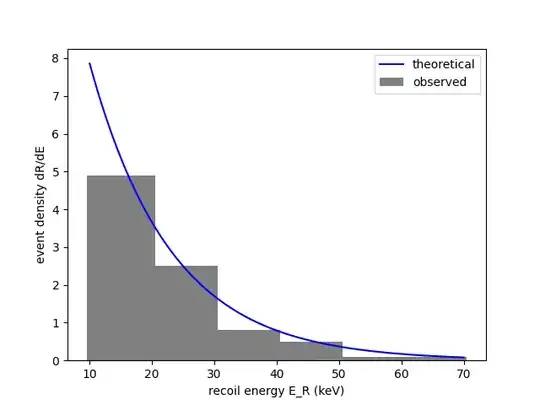
However, if I do a KS test as I've been taught on this, the highest difference (KS statistic) between the two distributions (at 10 keV) is rather high, so will give a fairly bad score, even though the distributions seem to match fairly well by eye. The KS statistic will also vary greatly with the bin width. Before I've only done KS tests on normal-type distributions which won't have this problem (at least as much). The same problem arises if you plot the cumulutive distribution.
I'm wondering if there's some way to overcome this high sensitivity at the bottom of an exponential distribution, or if there's some other test I should be using?