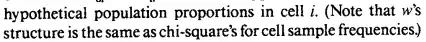Given a set of items of which each item is once measured using a computative model, each time under a different condition, what is the best way to quantify the magnitude of difference between measurements taken under different conditions?
My goal is to illustrate that there is no practical difference in measurements across these models when conditions change, and not just to illustrate a significant difference between one group mean and that of any other group at a certain set alpha and beta. A rejection of the null-hypothesis upon testing for differences in group-means in practice does not always seem informative, especially given large sample sizes, skewed and "taily" data and and small differences between group means and medians.
For example: Although the measurement methods described below in my practical case yield nearly identical measurements of the phenomena, an analysis using the Friedman-test leads to a rejection of the null-hypothesis (test statistic of 2977.98 with p-value <<0.001 using; https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.friedmanchisquare.html) as well as with a RM ANOVA (F=33.3, p-value <<.01 using; https://www.statsmodels.org/stable/generated/statsmodels.stats.anova.AnovaRM.html).
Towards this goal, given a single continuous variable as outcome, paired data/repeated measures, equal group sizes, no replications, what could be an appropriate alternative to performing a ANOVA (KW ANOVA, RM ANOVA or Friedman-test) to determine presence of any group mean differences followed by the appropriate post hoc procedures to pairwise determine which group means significantly from each other?
My data has >1000 images automatically assessed by a computational model for a single quantitative feature under six different methods (e.g. an automated assessment of % lung emphysema based on X-ray, where in each repeated measurement one of six types of noise is present in the image). The outcome variable is normally distributed around the median, but not around the mean across the six groups.
Crudely put, I am looking for a way to illustrate "robustness" or sustained precision of the measuring instrument under changing condition. It being able to produce measurements on a given item under different conditions.
A significant difference in group means in some practical cases does not imply at all a practical difference. Given the absence of a ground truth, what approach can be done to comprehensively illustrate that this set of methods yields measurements that are in strong accordance with each other besides the above approach or simply reporting CIs and pairwise correlation coefficients? Is reporting average within-subject variability not descriptive enough? Thank you for any input!