For normally distributed random variables, if X is independent of Y and X is independent of Z, is X independent of max(Y,Z)?

Question

Suppose $X,Y,Z\sim N(0,\sigma^2)$. $X$ is independent of $Y,$ $X$ is independent of $Z$ (but $Y$ and $Z$ are not independent), is $X$ independent of $\max(Y,Z)$?

Answer 1

If $X$ were not independent of $\max(Y,Z),$ that would seem to contradict a basic theorem that when two variables $U$ and $V$ are independent, then measurable functions of them $f(U),$ $g(V)$ are necessarily independent. That applies here to $U=X$ and $V=(Y,Z)$ with $f$ the identity and $g$ the maximum function. I suppose such a counterexample, if it exists, must involve a case where $X$ is not independent of $(Y,Z)$ even though $(X,Y)$ and $(X,Z)$ are independent. There is a standard example of that, which I will briefly describe.

Let $(U,V,W)$ be independent standard Normal variables. Define $S$ to be the sign of $UVW:$ that is, $S=1$ when $UVW \ge 0$ and otherwise $S=-1.$ Set $(X,Y,Z)=(SU,SV,SW).$ This guarantees $XYZ\ge 0,$ as you can readily check.

It is straightforward to check that all three pairs $(X,Y),$ $(X,Z),$ and $(Y,Z)$ have standard binormal distributions: in particular, all three pairs are independent. However, consider the case $\max(Y,Z)\lt 0.$ A negative maximum requires both $Y$ and $Z$ to be negative. Yet, because $XYZ\ge 0,$ $X$ must be positive.

Since the unconditional distribution of $X$ is Normal, it has positive chances of being negative. Consequently, conditioning $X$ on the event $Y\lt 0, Z \lt 0$ has changed the probability distribution of $X.$ Since the conditioning event does not have zero probability $$\Pr(\max(Y,Z)\lt 0)=\Pr(Y\lt 0,Z\lt 0)=\Pr(Y\lt 0)\Pr(Z\lt 0) = \left(\frac{1}{2}\right) \left(\frac{1}{2}\right) = \frac{1}{4},$$ it demonstrates a lack of independence between $X$ and $\max(Y,Z),$ QED.

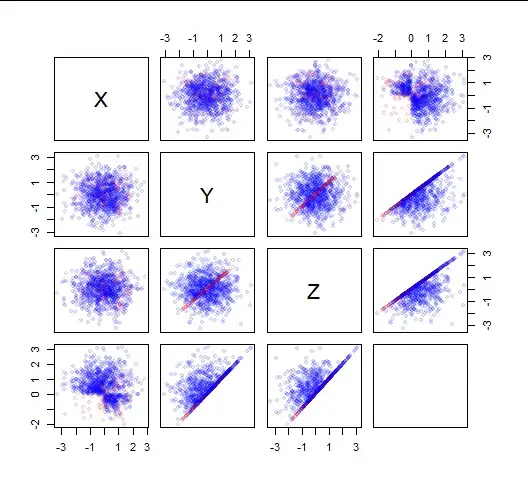
Here is a scatterplot matrix of one thousand draws from $(X,Y,Z,\max(Y,Z)).$ The circular clouds indicate independent pairs, while the distorted clouds demonstrate lack of independence.

We are not quite done. The question asks about the case where $(Y,Z)$ is not independent, whereas in this example $(Y,Z)$ is independent. We can fix that by using a mixture of the previous example and another one. Consider, for instance, the distribution of $(X_1, Y_1, Y_1)$ where $(X_1,Y_1)$ is standard Normal. A mixture of this "contaminating distribution" with the previous one does the trick.

Rather than dwelling on the mathematical details, let me just show you a couple thousand observations from this mixed distribution which is 90% the original example (blue dots) and 10% of the contaminating distribution (red dots).

The top row has the key characteristics of the previous example--especially an obvious lack of independence between $X$ and $\max(Y,Z)$ (the correlation coefficient is around $-0.19,$ far from zero), but now the $Y,Z$ scatterplots show lines of red dots, demonstrating the lack of independence of $(Y,Z).$