At first if I fail, ....should I keep trying

Question

The final goal is to predict the effect of intervention(A) on outcome(Y) in the presence of some confounders (x). Before running the model to evaluate the effect of A on Y, I am doing some Exploratory Data Analysis (EDA) using linear regression at univariate level , Y~A+$x_1$, Y~A+$x_2$, Y~A+$x_3$.....Y~A+$x_p$ so on. I am not finding any signal, $A$ has no effect on $Y$ at univariate level. Does it makes sense to run the final model with all the variables ? Is there a mathematical explanation why adding more variables (X) might make matter worse when there is no signal at univariate level ?

Answer 1

Multidimensional patterns

You can have patterns in the data that are not clearly visible when you look at single variables.

• This is possible in linear regression like the example below.

  

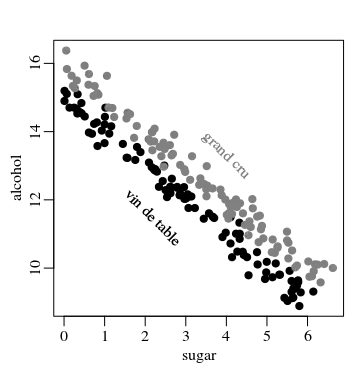
  In this figure there is a clear difference between the two types of wines. But if you'd look at only a single variable then the difference is not so clear.

• And there are even more possibilities when you have non-linear patterns like the next example

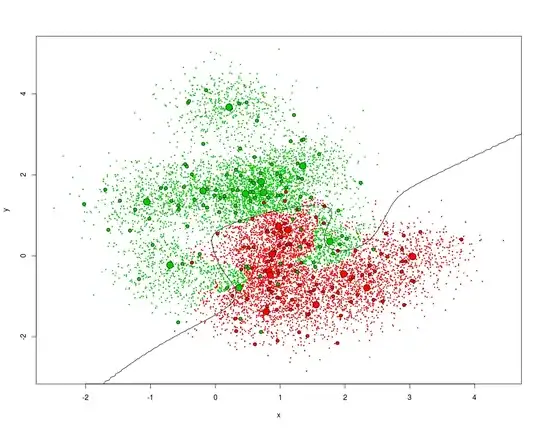  In this figure you see a nearest neighbours classification at work. The boundary is not a simple linear combination and many different patterns become possible.

Why adding confounders

Confounding variables are variables that both influence the treatment variable and the outcome variable.

This happens for instance in epidemiological research. For example, say you observe beer consumption and the occurrence of breast cancer, then these would have a negative correlation as being a woman is an important confounder that positively influences the probability of breast cancer but negatively influences the consumption of beer.

Controlling for non-confounding variables

In your question, you speak about an 'intervention' which sounds like a controlled experiment in which the other variables are not confounding variables as the intervention is made randomly and with no causal relation with the other variables.

The effect of controlling for other variables is to reduce the variation in the outcome that may be potentially caused by other variables and may be correlating with those other variables.

In this case, it might be that you do not observe a significant effect when you control for only a single variable and you might need to have more variables included.

For a single variable, you may have the situation below

The histograms on the right show that there is little difference in the outcome for the two treatment groups.

However, the scatter plot on the left shows that there is a difference. It is just that age has a much larger influence that makes the small effect of the treatment, not significant if the effect of the age is not taken into account (because the age becomes a large source of noise when it is not taken into account).

For multiple variables, you can imagine a similar situation but just with more variables. If the variables have a strong influence or at least are correlating a lot with the variation in the outcome, then you may need to add it as a control variable and just controlling one by one is not enough. (alternatively, if control variables have a lot of influence then it might be better to 'control' it and make sure that the experiment has little variation in this parameter)