I searched this on the internet, but barely found anything, and what I found was not satisfactory.
Quartile divides the data into 4 equal parts. Qi = i * (n+1)/4 where i=1, 2, 3
Decile divides the data into 10 equal parts. Di = i * (n+1)/10 where i=1, 2, ..., 8, 9
Precentile divides the data into 100 equal parts Pi = i * (n+1)/100 where i=1, 2, ..., 98, 99
where n are the number of observations
Why do Quartile, Decile, Percentile have plus 1 in their formula?
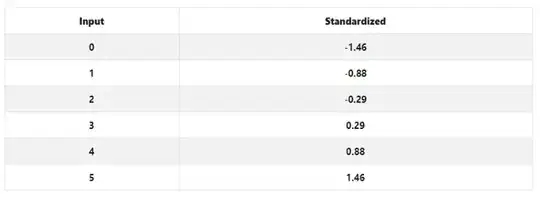
I will just take Q as an example, but the same can be extended to D and P. Let us assume there are 9 observations, so in my thought, the quartile should have been (see snapshot 1).
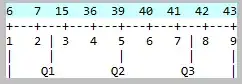
But by the formula, it comes out to be (see snapshot 2).
What this seems to have done is pushed the observations boundaries outside by 1 on both sides, then equally divided.
(Please ignore the blue row in the snapshots for now, they are just the value of the observations)
You see that the Q1 is nearer to the first observation and Q3 is nearer to the last observation by the plus 1 formula.
I see the same when we work with D and P, D1 and P1 are closer to the first observation, and D9 and P99 are closer to the last observation.
I want to understand what is going on here. Would greatly appreciate insights.