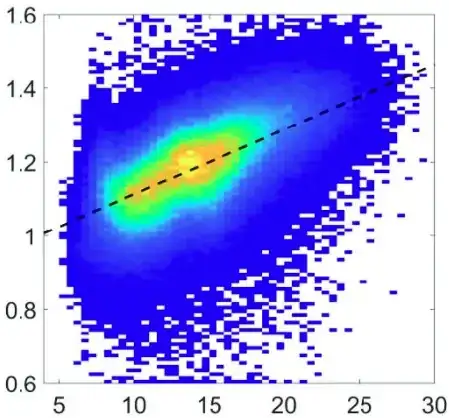
I've been looking into how to fit a line to a 2D histogram and have come across different pieces of information which I can't quite piece together. To show what I mean, I want to achieve something like the image below which is taken from a paper:
In the paper they refer to the line simply as the "linear regression result" but it is evidently not a regular linear regression as we are not dealing with just points in a plane as usual. They do not give further details on this that I could catch. I've seen plots like this in other places too even with confidence intervals for the regression line.
Looking around elsewhere I found this question in stack overflow. They advise OP to use the first principal component for the line which makes sense but this should be possible with regression as that is what they use in the paper. In the comments there is also some talk about "weighted least squares" which is a variant of ordinary least sqaures that is useful when the residuals show heteroscedasticity. However, I do not understand why this regression would be relevant to the problem or if thats what they are doing in the paper.