Questions about the constant value of the fixed-effect model in python PanelOLS

Question

I have a question about the constant value of the fixed-effect model.

I am currently conducting research through a fixed-effect model that controls the effects of each companies using Python's linearmodel package.

This is the result of Python and Stata when analyzing the same model.

It's not exactly the same, but you can see that most of the results are similar. However, in Stata result, one constant coefficient value and standard error value are shown, but python does not show constant.

In many research papers show constant values for the fixed-effect model, and I want to make that one intercept value and p-value can be obtained in my research.

I also looked up a lot of Internet data and looked for results like Stata's constant, but I couldn't find a way in Python (PanelOLS) or R (plm), so I'd like to ask many experts in this forum.

Thank you in advance.

[Code added]

import statsmodels.formula.api as smf
import statsmodels.api as sm
from linearmodels.panel import PanelOLS

model = PanelOLS.from_formula(‘Y ~ X1 + X2 + X3 + X4 + X5  + EntityEffects', data=df.set_index(['firm', 'date']))
results = model.fit(cov_type='clustered', cluster_entity=True)

Answer 1

If all you want is the intercept, then try extracting it manually. In Python's linearmodels package, try the params attribute, indexing by the constant term:

results = model.fit(...)
results.params['const']

Or, if you want all the estimated panel level effects, then try using the estimated_effects attribute:

results = model.fit(...)
results.estimated_effects

In my opinion, the git documentation is inexhaustive to say the least, but it should help to get you what you want.

---

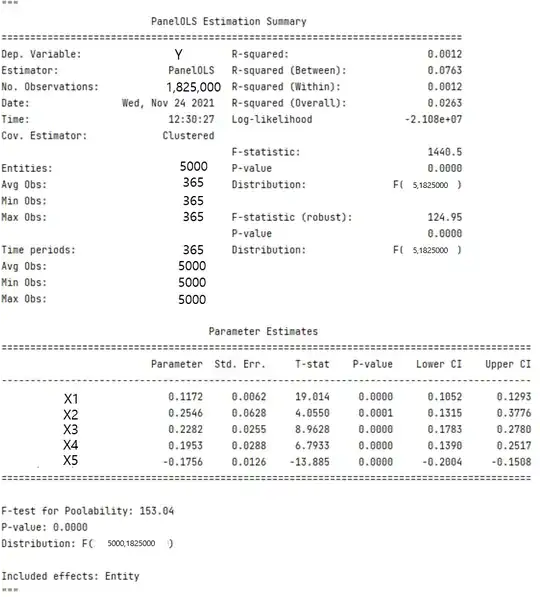
In Stata, the intercept is succinctly referred to as the "average value" of the fixed effects. To be clear, you're actually considering the following fixed effects model:

$$ y_{it} = \alpha + x_{it}'\beta + \mu_{i} + \epsilon_{it}, $$

where $\alpha$ is a global intercept (i.e., constant term) and $\mu_{i}$ denotes entity (e.g., individual, firm, state, etc.) fixed effects. Note how you cannot estimate a constant term and the entity-specific effects without imposing some kind of constraint. The constraint StataCorp places on the system is that the panel fixed effects sum to 0 across all observations in the sample.

In short, the "intercept" in -xtreg, fe- is the average of $\alpha + \mu_{i}$. Stata's support page discusses this in further detail.

---

R's plm package estimates a within model using the following equation:

$$ y_{it} = \alpha_{i} + x_{it}'\beta + \epsilon_{it}, $$

where $\alpha_{i}$ denotes entity fixed effects. This amounts to fitting a separate intercept for each unit in your panel. Note how the overall intercept parameter, $\alpha$ (unsubscripted), is not specified. In this context, $\alpha$ would be perfectly collinear with $\alpha_{i}$, as the sum of all the entity-specific effects (i.e., $\alpha_{i}$'s) is one. In R, we can extract these entity-specific intercepts (i.e., fixed effects) from a plm object using the fixef() function.

I should also note that a within_intercept() function is also available in the plm package. I always found it a bit artificial but it does return an "overall intercept" for within models and its accompanying standard error. Under the hood, it's simply a weighted mean of the fixed effects. Review my response here or this answer here for other R applications.

---

In sum, I wouldn't go looking for consistency across statistical software packages. In my opinion, the intercept is a trivial parameter in fixed effects applications. It's generally safe to omit.