Can a Probability Distribution ever "look similar" to a Cumulative Probability Distribution?
Suppose in some imaginary town - the height distribution of the residents are as follows:
- There are 100,000 residents between 220 cm and 200 cm
- There are 95,000 residents between 200 and 190 cm
- There are 90,000 residents between 190 and 180 cm
- There are 85,000 residents between 180 and 170 cm etc
Furthermore, the distribution is in such a way that the majority of the residents are always located in the tail end of each height range (e.g. In the 200 to 190 cm range, there are more residents closer to 200 cm than to 190 cm) : in general, you are more likely to meet a taller person than a shorter person.
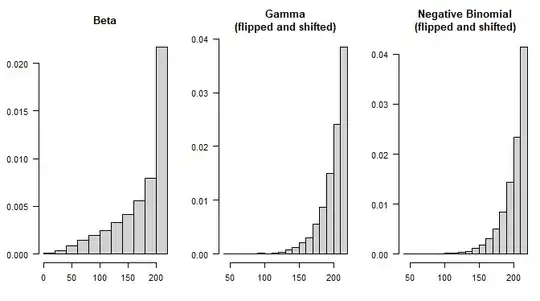
My Question: In general, what kind of probability distribution can describe this distribution in the data? The first that comes to mind is a "sigmoid" shaped Cumulative Distribution Function (e.g. Empirical Distribution Function):
But are there any probability distribution that can describe these types of height distributions listed above?
Above: Even in skewed distributions, the probability of observations being situated within the extreme tails still tends to be lower.
Above: Perhaps Binomial and Poisson Distributions can be used for modelling these kinds of distributions?
Thanks!
References: