Joint distribution where random variables always exist in the same orthant

Question

I am sampling two vectors $x$ and $y$ ($\in \mathbb{R}^n$). First, I sample $x$ from an isotropic Gaussian distribution. Then I want to sample $y$ from the same distribution, but only in the orthant where $x$ exists. For example, if the sampled $x$ is $$x=[0.4,0.3,0.2,-0.5] $$ we want to sample $y$ from a truncated Gaussian distribution that has zero probability everywhere except for the orthant where the signs are $[y_1>0,y_2>0,y_3>0,y_4<0]$.

How can I express $P(x,y)$?

I thought about expressing it first as $P(x,y|d) = P(x|d)P(y|d)$ where $d$ indicates an uniform random choice of an orthant, and $P(x|d)$ and $P(y|d)$ means that $x$ and $y$ are sampled from a Gaussian distribution truncated to just that orthant. Then, we calculate $P(x,y,d)=P(x|d)P(y|d)P(d)$ and marginalize out $d$. If there are $M$ orthants, than $P(d)=1/M$, so $$P(x,y)=\frac{1}{M}\sum_d P(x|d)P(y|d)P(d)$$ $$P(x,y)=\frac{1}{M}\sum_d P(x|d)P(y|d)\frac{1}{M}$$ $$P(x,y)=\frac{1}{M}M P(x|d)P(y|d)\frac{1}{M}$$ $$P(x,y)=\frac{1}{M}P(x|d)P(y|d)$$

Is this correct?

Answer 1

It depends on what you mean by "$P.$" Let's interpret this as asking for the joint probability density function.

Let the PDF of $X$ be $f.$ For instance, $f(\mathbf x) = (2\pi)^{-n/2}\exp(-||\mathbf x||^2/2)$ is its value for the standard Normal distribution in $\mathbb{R}^n.$

Define the function $s:\mathbb{R}^n\to \{-1,1\}^n$ to be the vector of signs of its arguments, letting (arbitrarily) the sign of $0$ be $+1.$ The $2^n$ possible values of $s$ correspond to the orthants, which (as events) I will denote $\mathcal{O}(\mathbf s).$

Let $Y$ be a random variable with PDF $g.$ When it is truncated to the orthant $\mathbf s = (s_1,s_2,\ldots,s_n)\in\{\pm 1\}^n,$ its PDF is restricted to that orthant and renormalized to integrate to unity. Thus, in terms of the indicator function $I,$ its truncated PDF is

$$g_{\mathbf s}(\mathbf{y}) = \frac{g(\mathbf{y}) I(s(\mathbf y) = \mathbf s)}{\int\cdots\int_{\mathcal{O}(\mathbf{s})} g(\mathbf{y}^\prime)\,\mathbf{\mathrm{d}}\mathbf{y}^\prime}.\tag{*}$$

(Recall that the value of $I$ at a true argument is $1$ and otherwise the value of $I$ is $0.$ Thus, $I(s(\mathbf y)=\mathbf s)) = 1$ when $\mathbf y$ lies in the $\mathbf s$ orthant and otherwise $I(s(\mathbf y)=\mathbf s)) = 0.$)

The construction in the question generates $Y$ conditional on $X$ with the distribution having $g_\mathbf{s(X)}$ for its PDF. ($\mathbf{s}(X)$ is all in the subscript! This is a function, not the value $g_{\mathbf{s}}(X).$) Consequently, the joint PDF is the product of the PDF of $X$ and this conditional distribution,

$$f_{X,Y}(\mathbf x, \mathbf y) = f(\mathbf x) g_\mathbf{s(\mathbf x)}(\mathbf y).$$

The specifics of the question permit a little bit of simplification because (assuming "isotropic" also means centered at the origin), the reflection symmetries of $g$ around the coordinate hyperplanes (and the fact that $g$ assigns zero probability to the union of those hyperplanes, allowing us to skirt any analysis of what happens with coordinates equal to zero) guarantee all the integrals in the denominators of $(*)$ are equal, whence they must all equal $2^{-n}$ (because there are $2^n$ distinct orthants and the total is $1$). One might then write

$$f_{X,Y}(\mathbf x, \mathbf y) = 2^n\, f(\mathbf x)\,g(\mathbf y)\,I(s(\mathbf y) = s(\mathbf x)).$$

Specializing even further to the case where $f=g$ is the PDF of the Normal distribution centered at the origin with variance $\sigma^2$ times the identity matrix, the example provided earlier (in the second paragraph of this answer) yields

$$f_{X,Y}(\mathbf x,\mathbf y) = \frac{I(s(\mathbf y) = s(\mathbf x))}{(\pi\sigma^2)^n} e^{\left(-||\mathbf x||^2 + ||\mathbf y||^2\right)/(2\sigma^2)}.$$

This looks just like the spherical Normal distribution on $\mathbb{R}^{2n}$ (with coordinates $(\mathbf x, \mathbf y)$ except it has been truncated to the region where the signs of the first $n$ components equal the signs of the second $n$ components.

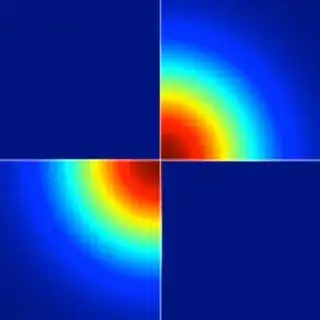
For instance, when $n=1$ this is the density

$$f_{X,Y}(x,y) = \frac{1}{\pi\sigma^2} e^{-(x^2+y^2)/(2\sigma^2)}$$

in $\mathbb{R}^2$ when $x$ and $y$ have the same signs (that is, lie in the first or third quadrants) and otherwise $f_{X,Y}(x,y)=0.$ It is illustrated in the upper right corner of the figure in Cardinal's examples of non-Normal bivariate distributions with Normal marginals: