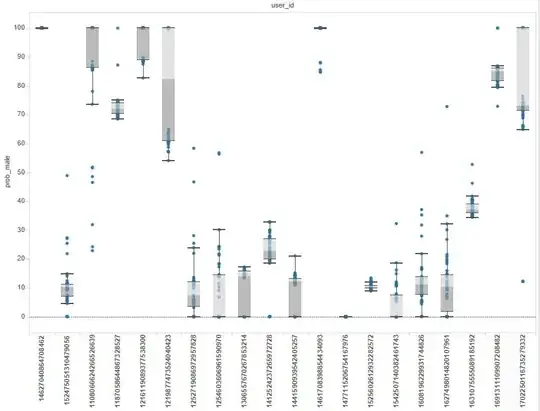
There are actually several equivalent expressions for these quantities.
Consider the linear regression model
$$y=\alpha+\beta_2 x+\beta_3 z +\varepsilon \tag{$\star$}$$
Parameters $\alpha,\beta_2,\beta_3$ are such that the mean squared error $\operatorname E(\varepsilon^2)$ is minimized.
Let's define some of the notation here. I denote $(y,x,z)$ in subscripts by $(1,2,3)$ for convenience. So $\sigma_y=\sigma_1$ is the (population) standard deviation of $y$. Similarly, $\sigma_{yx}=\sigma_{12}$ is the (population) covariance between $y$ and $x$. Also, $\beta_{yx}=\beta_{12}$ is the (population) regression coefficient of $y$ on $x$.
Accordingly, we may rewrite $(\star)$ as
$$y=y_{1.23}+\varepsilon_{1.23}\,, \tag{$\star\star$}$$
where $y_{1.23}=\alpha+\beta_2 x+\beta_3 z$ is the part of $y$ explained by $(x,z)$ and $\varepsilon_{1.23}=\varepsilon$ is the unexplained part.
Define $R=(\rho_{ij})_{1\le i,j\le 3}$ as the (population) correlation matrix of $(y,x,z)$ and let $R_{ij}$ be the cofactor of $\rho_{ij}$. Similarly, define $\Sigma=(\sigma_{ij})_{1\le i,j\le 3}$ as the (population) dispersion matrix with $\sigma_{ii}=\sigma_i^2$ and let $\Sigma_{ij}$ be the cofactor of $\sigma_{ij}$.
Then $\beta_{yx.z}=\beta_{12.3}(=\beta_2)$ is the partial regression coefficient of $y$ on $x$ eliminating the linear effect of $z$, which satisfies
$$\boxed{\beta_{12.3}=-\frac{R_{12}}{R_{11}}\cdot \frac{\sigma_1}{\sigma_2}} \tag{1}$$
This explains the formula
$$\beta_{12.3}=\left(\frac{\rho_{21}-\rho_{31}\rho_{23}}{1-\rho_{23}^2}\right)\frac{\sigma_1}{\sigma_2} \tag{1.a}$$
Or in terms of the dispersion matrix, it follows from $(1)$ and $(1.\text a)$ that
$$\boxed{\beta_{12.3}=-\frac{\Sigma_{12}}{\Sigma_{11}}} \tag{2}$$
and
$$\beta_{12.3}=\frac{\sigma_{21}\sigma_3^2-\sigma_{31}\sigma_{23}}{\sigma_2^2\sigma_3^2-\sigma_{23}^2} \tag{2.a}$$
Using $\beta_{1j}=\rho_{1j}\cdot \frac{\sigma_1}{\sigma_j}$ for $j=2,3$ and $\beta_{32}=\rho_{23}\cdot \frac{\sigma_3}{\sigma_2}$ in $(2.\text a)$, one gets
$$\beta_{12.3}=\frac{\beta_{12}-\beta_{13}\beta_{32}}{1-\beta^2_{32}\sigma_2^2/\sigma_3^2} \tag{2.b}$$
Analogous to $(\star\star)$, consider
$$y=y_{1.3}+\varepsilon_{1.3}\quad,\quad x=x_{2.3}+\varepsilon_{2.3}$$
Here $\varepsilon_{1.3}$ is the part of $y$ eliminating the linear effect of $z$, and $\varepsilon_{2.3}$ is the part of $x$ eliminating the linear effect of $z$. Then $\sigma_{yx.z}=\sigma_{12.3}$ is the partial covariance between $y$ and $x$ eliminating the effect of $z$, defined as
$$\sigma_{12.3}=\operatorname{Cov}(\varepsilon_{1.3},\varepsilon_{2.3})$$
Using normal equations, it is not difficult to show from this definition that
$$\boxed{\sigma_{12.3}=-\frac{\Sigma_{12}}{\sigma_3^2}} \tag{3}$$
This gives the formula
$$\sigma_{12.3}=\sigma_{21}-\frac{\sigma_{31}\sigma_{23}}{\sigma_3^2} \tag{3.a}$$
Again, from $$\beta_{12.3}=\frac{\operatorname{Cov}(\varepsilon_{1.3},\varepsilon_{2.3})}{\operatorname{Var}(\varepsilon_{2.3})}=\frac{\sigma_{12.3}}{\sigma^2_{2.3}}\,,$$
we have
$$\sigma_{12.3}=\beta_{12.3}\cdot\sigma^2_{2.3} \tag{4}$$
It can be shown that
$$\boxed{\sigma^2_{2.3}=\frac{\Sigma_{11}}{\sigma_3^2}}$$
Equivalently,
$$\sigma^2_{2.3}=\frac{\sigma_2^2\sigma_3^2 R_{11}}{\sigma_3^2}=\sigma_2^2(1-\rho^2_{23})=\sigma_2^2\left(1-\beta_{32}^2\cdot\frac{\sigma_2^2}{\sigma_3^2}\right) \tag{4.a}$$
Combining $(4.\text a)$ with $(4)$ and $(2.\text b)$ yields
$$\sigma_{12.3}=\sigma_2^2\left(\beta_{12}-\beta_{13}\beta_{32}\right) \tag{4.b}$$
Of course, this isn't the only way to justify the formulae in the original post. And as shown here, we can come up with many such formulae using different relationships between the coefficients.
For details regarding some of the derivations, one may refer to
Also see Multiple regression or partial correlation coefficient? And relations between the two.
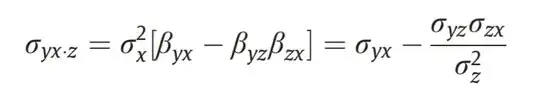 and
and