Edit: this question is not a duplicate of imposing a perpendicularity constraint in Gaussian linear regression. Here, the question is about hierarchical reference of the breakpoint position. The other question talks about imposing a condition on line perpendicularity at the breakpoint.
I'm trying to fit a piece-wise linear function to a dataset with one expected breakpoint using raw Python and Numpy.
I'm following the lectures by Dr. Philipp Hennig from Tübingen (https://www.youtube.com/watch?v=EF1BfKnINw0) and using his script as a base. Here is the sample data 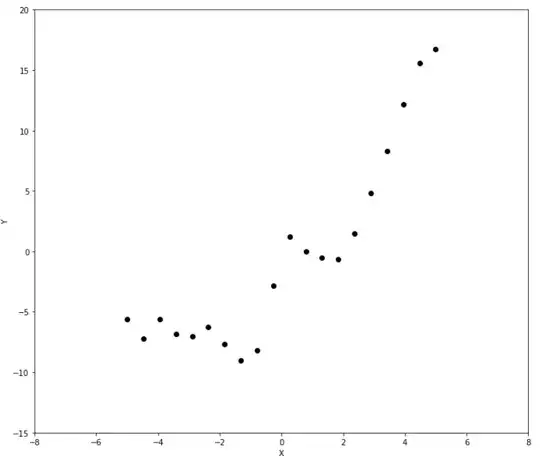 .
.
Here are the formulas that are implemented in the script: the prior on Y, likelihood of the weights, and the posterior on the weights and the resultant regression function: 
Here is the question.
In one of the following lectures it was mentioned that the inference on the parameters of a Gaussian Linear Regression can be done using hierarchical Bayesian inference as long as the model depends on the parameters in a linear fashion. I was hoping that someone would help me to figure out how to do it.
Let's call the $x = a$ the coordinate of the breakpoint, then we can expand the Bayesian inference to the following:
$$p(w | X, Y, a) = \frac{ p( Y | X, w, a) p (w | a) } { p( Y | X, a) } = \frac {p(Y | X, w, a) p(a | w) p (w) } { p( Y | X, a) p(a) }$$
where $w$ are weights. Here we can assume a Gaussian prior of the weights $p(w)$, just like in the formulas above we can derive an expression for the likelihood $p( Y | X, w, a)$, for $p( Y | X, a)$, but I can't come up with a way to describe $p(a|w)$ and $p(w)$. Does anybody have an idea how could I do that? Or any other ideas how to do find the breakpoint position analytically?
I also have an idea about how the breakpoint correlate with weights for $p(a|w)$. The lower is the weight for the first linear function, the lower is the $a$ value. However, I don't know how to express this analytically.
Current Solution
So far I used Principal Component Analysis to find the breakpoint position and the following feature set. The second linear feature comes into play at $x = a$ only.
$$ \phi_x = \begin{bmatrix} 1 \\ x \\ x \end{bmatrix} $$
With this I get the following sample solution:
I've done quite a bit of research and so far could not find a suitable analytical solution that does not use optimization techniques. I also had a look on the "Sample splitting and threshold estimation" by Hansen (1).
Disclaimer: this is my first question here and I'm very new to Bayesian statistics, so please be gentle :)
References:
(1) Hansen, B. E., May 2000. Sample splitting and threshold estimation. Econo- metrica 68 (3), 575–604.