I have a dataset that contains a couple of hundred results from a computational task related to plasma physics. The computation time of the task is, due to the high complexity of the underlying physics, in the order of weeks. I am tasked to come up with (non-linear) regression laws that capture some of the global results from the simulation, given certain input features. This way the outcomes of the simulation can be approximated, without having to go through weeks of computation. The regression laws are based on observed physical phenomena, as a complete black-box model that completely neglects the underlying physics is not desired here. This has worked for me so far, resulting in regression expressions that look for example like this:
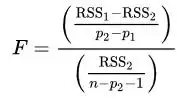
Where T is a global output parameter and mu, c, P_# and Pe/Pi are input parameters that are given to the simulation program. Using statistical tools, I was able to estimate uncertainties on these fittings as well. This gives desirable results, but still additional simulations will be needed to develop more reliable regression laws.
My question is now: given these uncertainties on the fittings and the limits on the input parameter space (i.e. the inputs must remain physical with regard to the problem), what would the best suggestion for a new simulation with chosen input parameters be, so that the uncertainty on the fittings is maximally reduced? I believe that the question is rather clear to me, but I have no idea on where to start . Is there anyone that has any experience on a simular problem that