How many coin flips are needed to reliably know a coin of weight w is unfair?

Question

I want to find out how many flips I need to flip a coin to reliably know that it is an unfair coin.

The issue is that as the coin becomes closer to 50/50, the more false-negatives you will have if you don't take dramatically more data.

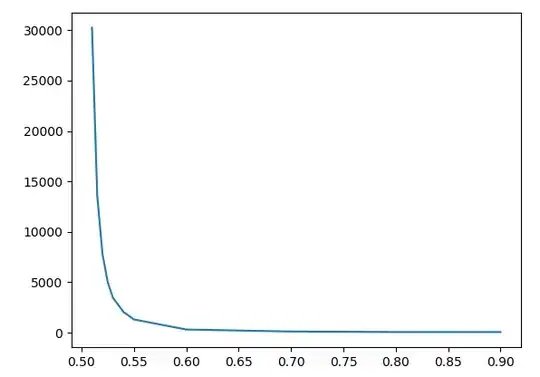
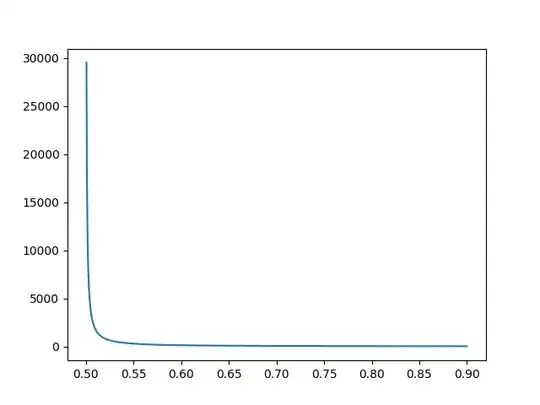
I wrote some python code and numerically found out how many flips are needed to be able to confirm a weighted coin with weight w. As w gets closer to .5, exponentially more flips are needed to have a low false-negative rate, as shown in this figure I made in python:

The x-axis represents the weight of the coin, while the y-axis represents the number of flips to get a false-negative rate of 5% (while also having a 5% false-positive rate).

Is there a way of getting this answer analytically? I'm particularly interested in what approximations can be done to know what will occur as you get closer to .5.

Here's my python code attempt that was used to generate the figure. I have added comments in the code to try to explain the logic:

from scipy import stats
import numpy as np
import matplotlib.pyplot as plt



# The goal of this script is to figure out how many flips are required to
# have a low false-negative rate when testing if a coin is fair for a specific
# p-value. I use this script to understand the relation between
# the unfairness of the coin and the amount of flips needed to get a low false-negative
# rate. 
# Essentially we calculate the false-negative rate for some starting number of flips,
# and if this rate is lower than our desired threshold, then we add more number of flips,
# we continue this in a loop until we are under the false-negative rate (or until we run 
# out of iterations)
# Finally, we run this all inside the function find_numberofFlips_and_false_negatives_vs_fairness
# this function has an input of the coins fairness, and returns a number of flips as an output
# we then use this function to collect a set of points for the coins fairness vs numberofFlips 
# then we plot this

def flipAndDoPTest(numberOfFlips, weight, guessWeight):
    """
    Simulate multiple coinflips and perform a binomial test, 
    returning a pvalue.
    
    Parameters
    ----------
    numberOfFlips : int
                    The number of flips that will be simulated.
    weight        : int
                    The weight of the coin that is flipped
    guessWeight   : float 
        The hypothesized probability of success, i.e. the expected
        proportion of successes. We will typically use .5 for this.
        
    Returns
    -------
    result :
        pvalue : float
            The p-value of the hypothesis test.
    """
        
    flippedCoinSimulation = np.random.binomial(1, weight, numberOfFlips) 
    numberOfHeads = np.sum(flippedCoinSimulation==1)
    numberOfTails = np.sum(flippedCoinSimulation==0)
    pvalue = stats.binom_test(numberOfHeads, numberOfFlips, guessWeight)
    return pvalue

def accurate_pvalue_interval(numberofFlips, desiredConfidenceLevel):
    """
    Creates an new confidence interval which is closest to the desiredConfidenceLevel.
    Because of the discrete nature of coin flips, it's not possible to get any arbitrary
    confidence level. This code finds the closest confidence level that has a pvalue lower
    than the desired confidence level.
    
    Parameters    
    ----------
    numberofFlips          : int
                             The number of flips that will be done for the 
                             relevant confidence level.
    desiredConfidenceLevel : float
                             the desiredConfidenceLevel that we will find the nearest
                             confidence level for
        
    Returns
    -------
    result :
        pValUnderThreshold : float
                             the nearest valid pvalue that is smaller than the desiredConfidenceLevel
            
    """
    
    numberofIntervals = np.int(np.round(numberofFlips/2));
    intervalIndex = np.arange(numberofIntervals);
    intervalList = 2*(stats.binom.cdf(intervalIndex,numberofFlips,.5));
    pValUnderThreshold = np.max(intervalList[intervalList <= desiredConfidenceLevel])
    return pValUnderThreshold


def false_negative_calculator(numberofFlips, unfairCoinWeight, desiredConfidenceLevel):
    """
    loop through each coin and do a simulated p-test to see if for a set number of coinflips 
    if the given coin is verified to be unfair in a confidence window.
    if the coin is a fair coin, and pvalue<=closestConfidenceLevel (meaning it passes the binomial test and 
    the coin is unfair in a certain confidence window), then we add 1 to the false-positive number
    if the coin is an unfair coin, yet is not identified as one, then we add1 to the false-negative numbers
    """
    guessWeight = .5
    falsePositives = 0
    falseNegatives = 0
    numberofTrials = 1000
    
    
    #for our p-test, we want to make sure to pick an interval that fits the discretness of 
    #the problem. Therefore we input a desired confidence interval, and the function finds 
    #the nearest confidence interval that can be used.
   
    closestConfidenceLevel = accurate_pvalue_interval(numberofFlips, desiredConfidenceLevel)
    
    #see how many false negatives are obtained in a number of trials.
    for ithTrial in range(numberofTrials):
        pvalue = flipAndDoPTest(numberofFlips, unfairCoinWeight, guessWeight)     
        if pvalue>closestConfidenceLevel:
            falseNegatives += 1
    falseNegativeRate = falseNegatives/numberofTrials            
    return falseNegativeRate


def find_numberofFlips_and_false_negatives_vs_fairness(unfairCoinWeight):

    numIterations = 1000
    #maximum number of iterations used in the loop
    numberofFlips = 10
    #initial starting number of flips used in the first iteration of loop
    flipNumberIncrement = 50
    #how much the flip number increases by each iteration in loop
    numberofStandardDeviationSeparation = 4
    #decides the amount of standard deviations the unfair coin is from the fair coin that we finding the 
    #number of flips for
    falseNegativeThreshold = .05
    desiredConfidenceLevel = .05

    #Loop explained in the function deviation_separation_calculator()
    for stepi in range(numIterations):
        falseNegativeRate = false_negative_calculator(numberofFlips, unfairCoinWeight, desiredConfidenceLevel)
        if falseNegativeRate <= falseNegativeThreshold:
            print("Completed in", stepi, "total increments and requires", numberofFlips, "number of flips", "with a false negative rate of:", round(falseNegativeRate*100, 4), "%")
            break
        else:
            numberofFlips += flipNumberIncrement
    if falseNegativeRate > falseNegativeThreshold:
        print("Could not find solution in the given number of iterations:", numIterations)
    return numberofFlips



    
weightList = np.array([.9, .8, .7, .6, .55, .54, .53, .525, .520, .515, .510])
#list of weights of the unfair coin; as this gets closer to .5 the more numberofFlips will be needed for
#our condition to be satisfied

numofFlipsList = np.arange(len(weightList))
for i in range(len(weightList)):
    numofFlipsList[i] = find_numberofFlips_and_false_negatives_vs_fairness(weightList[i])
    print("For fairness weight of:", weightList[i], "number of flips required is",numofFlipsList[i])

plt.plot(weightList, numofFlipsList)   

Answer 1

There are various ways you could examine this problem analytically, but a typical way is to frame the problem as a hypothesis test for a stipulated probability for the coin. Suppose we let $X_1,X_2,X_3, ... \sim \text{IID Bern}(\theta)$ denote the outcomes of the coin-flips where $\theta$ is the probability of flipping a head (here denoted by a one). We can use a classical binomial proportion test to test the hypotheses:

$$H_0: \theta = \tfrac{1}{2} \quad \quad \quad \quad \quad H_\text{A}: \theta \neq \tfrac{1}{2}.$$

There are various types of binomial test in statistical analysis, but the simplest is the Wald test, which uses the normal approximation to the binomial proportion. If you want to know how many flips you need to reliably detect an unfair coin, the usual thing to do would be to find out how many flips you need to obtain some minimum stipulated power against a specified value for the parameter that is close to the null value.

To do this you will need to specify three things: (1) the significance level for your hypothesis test; (2) the parameter value at which you want to compute the power (presumably a value close to your null value); and (3) the minimum power you will consider to be sufficient to constitute a "reliable" test. In the section below I give an example of this using the power function for the Wald test.

---

Computing sample size via power of the Wald binomial test: The two-sided Wald test for the null hypothesis $H_0: \theta = \tfrac{1}{2}$ uses the test statistic an approximate null distribution:

$$Z_n \equiv \sqrt{n} \cdot \frac{p_n - \tfrac{1}{2}}{\sqrt{p_n (1-p_n)}} \overset{\text{approx}}{\sim} \text{N}(0,1).$$

At significance level $0 < \alpha < 1$, the test has acceptance-region $-z_{\alpha/2} \leqslant Z_n \leqslant z_{\alpha/2}$, which can be rewritten as:

$$\bigg( p_n - \frac{1}{2} \bigg)^2 \leqslant z_{\alpha/2}^2 \cdot \frac{p_n (1-p_n)}{n},$$

which can be shown to be equivalent to $L(\alpha,n) \leqslant n p_n \leqslant U(\alpha,n)$ with the lower and upper bounds:

$$L(\alpha,n) \equiv \frac{n}{2} \Bigg[ 1 - \sqrt{\frac{z_{\alpha/2}^2}{n + z_{\alpha/2}^2}} \Bigg] \quad \quad \quad \quad \quad U(\alpha,n) \equiv \frac{n}{2} \Bigg[ 1 + \sqrt{\frac{z_{\alpha/2}^2}{n + z_{\alpha/2}^2}} \Bigg] .$$

Consequently, the exact power function for the test is:

$$\begin{align} \text{Power}_\alpha(\theta) &= 1 - \mathbb{P} ( \text{Accept } H_0 | \theta ) \\[6pt] &= 1 - \mathbb{P} ( L(\alpha,n) \leqslant n p_n \leqslant U(\alpha,n) | \theta ) \\[6pt] &= 1 - \sum_{L(\alpha,n) \leqslant x \leqslant U(\alpha,n)} \text{Bin} (x|n, \theta). \\[6pt] \end{align}$$

We can program this power function in R as follows (we have vectorised this function with respect to the input n to make the next step easier).

#Create power function for the Wald binomial test
power.binom.test <- function(n, prob, alpha = 0.05) {
  z2    <- qnorm(1-alpha/2)^2
  OUT   <- rep(0, length(n))
  for (i in 1:length(n)) {
    nn    <- n[i]
    TERM  <- sqrt(z2/(nn+z2))
    LOWER <- ceiling((nn/2)*(1-TERM))
    UPPER <- floor((nn/2)*(1+TERM))
    OUT[i] <- 1 - sum(dbinom(LOWER:UPPER, size = nn, prob = prob)) }
  OUT }

To compute the required sample size we need to specify the three elements discussed above. For illustrative purposes, let's stipulate that we are using a test with a 5% significance level and we want to compute the power at the point $\theta = 0.51$ and we require that the power at this point must be at least 90%.

#Set parameters for the computation
ALPHA     <- 0.05
THETA.ALT <- 0.51
MIN.POWER <- 0.9

#Compute required sample size
POWER     <- power.binom.test(n = 1:30000, prob = THETA.ALT, alpha = ALPHA)
SAMP.SIZE <- min(which(POWER >= MIN.POWER))

#Show required sample size
SAMP.SIZE
[1] 26226

In this case we see that we require a minimum sample size of $n = 26,226$ to have 90% power in detecting the alternative value $\theta_1 = 0.51$ using a Wald test with 5% significance level. This is just one example of this type of calculation, and you could use different numbers if you prefer.

Answer 2

We can simplify the power calculation by

• approximating the sample distributions as normal distributions with $$\sigma \approx \sqrt{pq/n}$$
• approximation $pq \approx 0.5^2$ such that $$\sigma\approx \frac{0.5}{\sqrt{n}}$$
• approximating the power by considering the entire left tail as non-rejection of the hypothesis (which is not entirely true because a tiny part of the tail is below the lower boundary, but this is very small)

So then we need that the distance $p-0.5$ is equal to $(1.96+1.65)\sigma$. Which leads to

$$p-0.5 = (1.96+1.65)\frac{0.5}{\sqrt{n}}$$

or

$$n = \left(\frac{(1.96+1.65)}{2p-1} \right)^2$$

These values $1.96$ and $1.65$ are computed by the quantile function of the normal distribution and relate to the $2.5\%$ and $5\%$ quantiles.

If we get rid of the second approximation (the deviation is computed for both null and alternative hypotheses with $p=0.5$) then the solution will become

$$n = \left(\frac{0.5 \cdot 1.96 + \sqrt{p(1-p)} \cdot 1.65}{p-0.5} \right)^2$$

---

Computational comparison

In the graph below we compare the approximation with exact computations

The used code is in R but I imagine it is easy to read and can be easily converted into python.

###
### function to compute power 
### for given sample size n
### and given effect p
###
power = function(n,p) {
  ### hypothesis test boundaries based on binomial distribution quantiles
  lower = qbinom(0.025,n,0.5) ### this gives a lower/left tail of at least 2.5%
  upper = n-(lower+1) ### make a symmetric upper/right tail
  
  ### compute power as probabilities of rejection
  ### two parts either we are below the lower boundary or above the upper boundary
  pbelow = pbinom(lower-1,n,p) # reject when below 'lower' 
  pabove = 1-pbinom(upper,n,p) # reject when above 'upper'
  
  ### return total probability of rejection
  return(pbelow+pabove)
}

### function to get required 'n' 
### such that type 2 error is below 5% (or power above 95%)
get_n = function(p,start_n) {
  
  ### get the value of neccesary 'n' with a loop
  ### we start with start_n and keep increasing n untill the power is above 0.95
  n_test = start_n 
  while (power(n_test,p) < 0.95) {
    n_test = n_test + 1
  }
  
  return(n_test)
}


### plot the theoretic curve
n = 1:30000
plot(0.5+(qnorm(0.975)+qnorm(0.95))*sqrt(n*0.5^2)/n,n, type = "l", xlim = c(0.5,1),
     xlab="p", ylab = "", yaxt = "n")
### y axis tags and label
axis(2, at = 5000*c(0:10), las = 2) ## 
mtext("n", 2, line=4, las = 2)

n_current = 1
### add computed points
for (p in c(0.9, 0.8, 0.7, 0.6, 0.55, 0.54, 0.53, 0.525, 0.520, 0.515, 0.510)) {
  ### compute the neccesary n
  ### and use the old n_current to optimize the loop in the get_n function
  n_current = get_n(p,n_current)
  points(p, n_current)
} 

Answer 3

We use the likelihood method. Suppose that you have that

$$\mathcal{P}(X_n = 1 ) = p$$

for some $p \in [0,1]$. Then the likelihood that you will see the sequence of coinflips $X=X_1...X_n = s_1...s_n=s$

$$\mathcal{P}^{(n)}(X = s) = p^{\mathcal{N}_1(s)}(1-p)^{\mathcal{N}_0(s)} $$

where $\mathcal{N}_i(s)$ is the number of $i$'s in $s$. Thus the likelihood function for $X$ is $$\mathcal{L}^{(n)}(s,p) = p^{\mathcal{N}_1(s)}(1-p)^{\mathcal{N}_0(s)} $$ and we further have that $$ -\frac{1}{n}\mathcal{l}(s,p)= -\frac{1}{n}\log\mathcal{L}(s,p) = \frac{\mathcal{N}_1(s)}{n}\log_2p +\frac{\mathcal{N}_0(s)}{n}\log_2(1-p) .$$

Now we use the Asymptotic equipartition property that the Typical set possesses to get that if we let $$\mathcal{H}(p ) = p \log_2p +(1-p)\log_2(1-p) $$ and let $$\mathcal{A}_{\epsilon}^{(n)} = \{ s \in [0,1]^n \mid -\frac{1}{n}\mathcal{l}(s,p) \in ( \mathcal{H}(p ) - \epsilon , \mathcal{H}(p ) + \epsilon ) \}$$ then the probability $$\mathcal{P}(X \in \mathcal{A}_{\epsilon}^{(n)}) \geq 1 - \epsilon $$ holds by Asymptotic equipartition property that the Typical set possesses for large $n$. How Large does the $n$ have to be?

Edit:

Use theorem 11.2.1 in "Elements of Information" Cover & Thomas to get that the probability that the string of coinflips will be atypical will be $$ P(X \notin \mathcal{A}_{\epsilon}^{(n)}) \leq 2^{2\log(n+1)-n\frac{\mathcal{H}(0.5)-\mathcal{H}(p)}{2}} $$ if I interpret the test as follows: I flip the coin $n$ times; if the string of coinflips $s$ is in $\mathcal{A}_{\epsilon}^{(n)}$ then we declare it fair if not we declare it unfair. By choosing $\epsilon < \frac{\mathcal{H}(0.5)-\mathcal{H}(p)}{2}$ we guarantee that the two sets $\mathcal{A}_{\epsilon}^{(n)}$ for the fair and unfair coin are disjoint and thus the previous bound holds regardless of whether the coin is fair or not since $ P(X \notin \mathcal{A}_{\epsilon}^{(n)}) = 2^{2\log(n+1)-n\epsilon } $ by theorem 11.2.1 in "Elements of Information".

The graph you gave is then given by $$ f(p)= \min_n \{n \in \mathbb{N} \mid 2^{2\log(n+1)-n\frac{\mathcal{H}(0.5)-\mathcal{H}(p)}{2}} \leq 0.05\}. $$ The analytic result you are looking for can probably be proven by looking for an analytic proof that $$ |p-0.5|< \Delta^{-1} \implies f(p)=\mathcal{\Omega}(2^{\Delta}) $$ or some other interesting lower bound $B$; i.e., $f(p)= \mathcal{\Omega}(B({\Delta}))$.

Edit #2

The following python code:

import matplotlib.pyplot as plt
import math

def h(p):
    return -p*math.log(p,2)-(1-p)*math.log(p,2)

def solve(f,bound):
    k = 0
    sol = 2**k
    while f(sol) > bound:
        k += 1
        sol = 2**k
    if k == 0:
        return 1
    sol = sol // 2
    for i in range(k):
        if f(sol + 2**(k-i-1)) > bound:
            sol += 2**(k-i-1)
    if f(sol) > bound:
        sol+=1
    return sol

def failure_probability(n,p):
    return 2**(2*math.log(n+1,2)-n*((1-h(p))/2))

def fail_prob_for_n(p):
    return lambda n : failure_probability(n,p)

bound     = 0.05
d         = 0.0001
min_prob  = 0.5006
max_prob  = 0.9
num_ints  = int((max_prob - min_prob)/d)
x = []
y = []
for i in range(num_ints):
  p = max_prob-d*i
  n = solve(fail_prob_for_n(p), bound)
  x.append(p)
  y.append(n)

plt.plot(x,y)
plt.savefig('coin_flip.png')

gives the following plot:

This is nearly identical to your plot and it gives a precise information-theoretic provable bound. This python code finds the integer that satisfies the $0.05$ bound you are looking for in $\mathcal{O}(\log(n)^2)$ time since it uses successive squaring as an optimization.

Edit #3

We can now prove that $$ |p-0.5|< 2^{-k} , \ x>0\implies f(p)=\mathcal{O}(2^{(2+x)k}) $$ as well as $$ |p-0.5|< 2^{-k} \implies = \mathcal{\Omega}(2^{2k}). $$ To this end notice that $|p-0.5|< 2^{-k}$ and $n = 2^{(2+x)k}$ implies $$ P(X \notin \mathcal{A}_{\epsilon}^{(n)}) \leq 2^{2\log(2^{(2+x)k}+1)-2^{(2+x)k-1}(1+(0.5+2^{-k})\log (0.5+2^{-k}) + (0.5-2^{-k})\log(0.5-2^{-k}))} $$ and that $$\lim_{k \to \infty } \frac{1+(0.5+2^{-k})\log_2(0.5+2^{-k})+(0.5-2^{-k})\log_2(0.5-2^{-k})}{2^{-2k}} = 2.88539 $$ implies that $$ \lim_{k \to \infty} 2^{2\log(2^{(2+x)k}+1)-2^{(2+x)k-1}(1+(0.5+2^{-k})\log (0.5+2^{-k}) + (0.5-2^{-k})\log(0.5-2^{-k}))} = 0 ; $$

thus, we have that $$ f(p)=\mathcal{O}(2^{(2+x)k}) $$ for any $x>0$ as was desired.

We further see that the limit fails when $x=0$ so that $$ f(p)=\mathcal{\Omega}(2^{2k}) $$and thus we have that $$ |p-0.5|< \Delta^{-1} \implies n = \mathcal{O}(\Delta^{(2+x)}) $$ and that $$ |p-0.5|< \Delta^{-1} \implies n = > \mathcal{\Omega}(\Delta^{2}) $$ which gives upper and lower bounds on the number of coinflips