Calibration
For completeness sake, here are two other ways to produce calibration plots: The first is using calibration belts, introduced by Nattino et al. (2014)$^{1}$, Nattino et al. (2016)$^{2}$ and Nattino et al. (2017)$^{3}$. Briefly, they fit an $m$-th-order polynomial logistic function (with $m\geq 2$) to the observed outcomes using the predicted probabilities of the model to be assessed. The parameter $m$ is selected using a standard forward selection procedure controlled by a likelihood-ratio statistic that accounts for the forward process used to select $m$. The calibration belt can be used for internal and external calibration. The procedure is implemented in Stata (calibrationbelt) and R (package givitiR). Here is the example using the Challenger data:
# Challenger Shuttle Challenger temp vs oring-ok
dat <- data.frame(y=c(0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 1,
0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1),
x=c(53, 57, 58, 63, 66, 67, 67, 67, 68, 69, 70, 70,
70, 70, 72, 73, 75, 75, 76, 76, 78, 79, 81))
fit <- glm(y ~ x, data=dat, family=binomial)
preds_p <- predict(fit, type = "response")
cb <- givitiCalibrationBelt(o = dat$y, e = preds_p , devel = "internal", confLevels = c(0.95, 0.8))
plot(cb, main = "", las = 1, ylab = "Observed probabilities", xlab = "Model probabilities", table = FALSE)

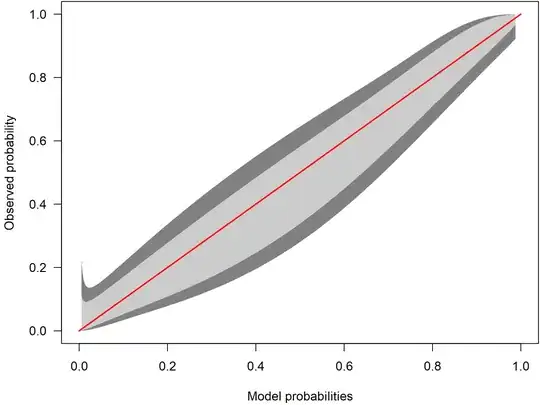
The identity line is displayed in red. The light gray area is the 80% confidence calibration interval whereas the dark gray is a 95% confidence interval. Ideally, the red line is inside the belt over the whole range of probabilities. In the example, the confidence intervals are huge: The calibration belt shows a large uncertainty with respect to calibration. As the red line lies within the interval, we cannot reject the hypothesis of a well calibrated model.
To better illustrate the calibration belt, let's look at a calibration belt of a well calibrated model:
Here, the confidence intervals are much narrower. Because the red identity line lies within the belt over the whole range, it offers little evidence for miscalibration.
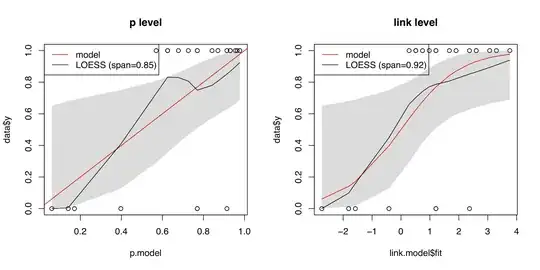
As some of the other answers, the second method implemented in the R package rms relies on a nonparametric smoother fitted to the predicted and observed probabilities. It also plots bias-corrected estimates based on the bootstrap. Details can be found in Harrel (2015)$^{4}$.
library(rms)
mod <- lrm(y~x, dat = dat, x = TRUE, y = TRUE)
res <- calibrate(mod, B = 10000)
plot(res)
The model seems to underestimate probabilities lower than $0.75$ and overestimate probabilities in over $0.75$. But again, due to the small sample size, the uncertainty is large.
Residuals
There are many types of residuals for generalized linear models but their interpretation is often difficult. One possibility is to look at simulation-based quantile residuals as implemented in the DHARMa package for R. Here is the example using the same data as above:
fit <- glm(y ~ x, data=dat, family=binomial)
simres <- simulateResiduals(fit, n = 1e4, seed = 142857)
plot(simres)
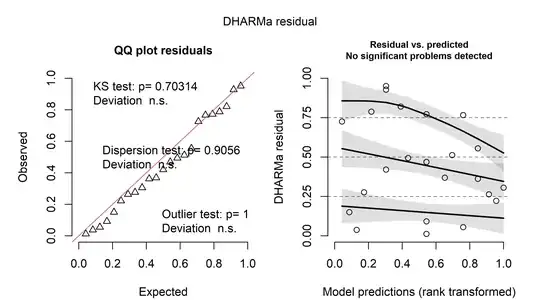
The nice thing about these residuals is that they can be interpreted as the "usual" residuals from linear regression models. On the left, a Q-Q-plot of the residuals is shown. On the right, the residuals are plotted against the predicted values. In both cases, there seems to be little evidence for a problem.
$[1]:$ Nattino, G., Finazzi, S., & Bertolini, G. (2014). A new calibration test and a reappraisal of the calibration belt for the assessment of prediction models based on dichotomous outcomes. Statistics in medicine, 33(14), 2390-2407.
$[2]:$ Nattino, G., Finazzi, S., & Bertolini, G. (2016). A new test and graphical tool to assess the goodness of fit of logistic regression models. Statistics in medicine, 35(5), 709-720.
$[3]:$ Nattino, G., Lemeshow, S., Phillips, G., Finazzi, S., & Bertolini, G. (2017). Assessing the calibration of dichotomous outcome models with the calibration belt. The Stata Journal, 17(4), 1003-1014.
$[4]:$ Harrell, F. E. (2015). Regression modeling strategies: with applications to linear models, logistic and ordinal regression, and survival analysis (Vol. 3). New York: springer.