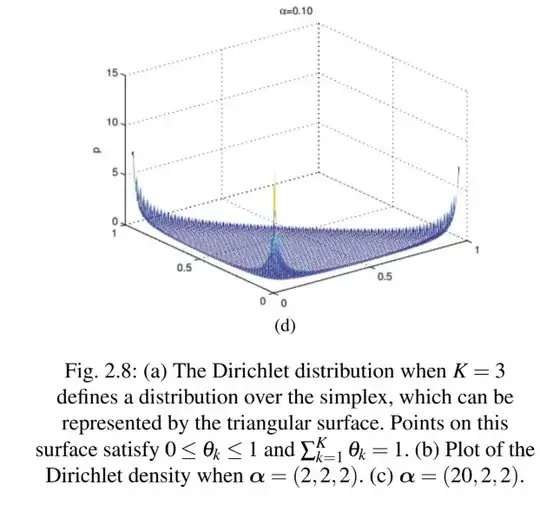
Recently, I came across the following image of a "probability distribution" defined over a "simplex":
Question: In the above picture, what exactly is the "simplex"?
I tried reading about the official definition of a "simplex":
However, I can't seem to understand the relationship between the "simplex" in which the probability distribution is defined compared to the official definition of the "simplex".
Can someone please help me understand what exactly is a "simplex" in this context? Does this "simplex" have any relationship to the "simplex method" (https://en.wikipedia.org/wiki/Simplex_algorithm) in optimization and linear programming?
References: