Background: As I understand the role of probability in Quantum Mechanics, the idea is that no observable event can have negative probability, but that it can make sense for unobserved quantities to have negative probability, so long as when marginalizing over unobserved events we obtain a proper probability distribution over observable ones.
Bayesian hierarchical models often contain unobservable latent variables. Conceivably, endowing some of these latent variables negative probability (densities) could still result in a well defined probability density over the observable nodes. And, also conceivably, doing so would allow for a more parsimonious description of the marginal probability distribution than is possible using latent variables with positive probabilities only.
More Background: Maybe an example is in order. Let's consider the standard two-cluster Gaussian mixture model with unknown mean and identical, known variance in dimension 1, for now with positive probabilities as usual:
$$z \sim bern(\rho)$$
$$y|z=0 \sim N(\mu_0,1)$$
$$y|z=1 \sim N(\mu_1,1)$$
Here, the unobserved latent variable is $z$, and when marginilizing over it, we are left with:
$$\delta_y(y) = \rho \delta_{N(\mu_0,1)}(y) + (1-\rho) \delta_{N(\mu_1,1)}(y)$$
where $\delta_y$ is the density of $y$ and $\delta_{N(a,b)}$ gives the density of a normal distribution with mean $a$ and variance $b$.
Here's what that density looks like for $\mu_0=1$,$\mu_1=-1$ and $\rho=0.9$:
(Since the peaks are close relative to the standard error it looks much like a single normal distribution).
Now I'm going to change the second density from being a $N(\mu_1,1)$ to a distribution with negative probabilities by changing it's density to this function:
$$\delta_{\aleph} := \delta_{N(\mu_1,0)}\textrm{sgn}(\mu_1-y)$$
where $\textrm{sgn}(a)$ is the sign function, so it looks like this:
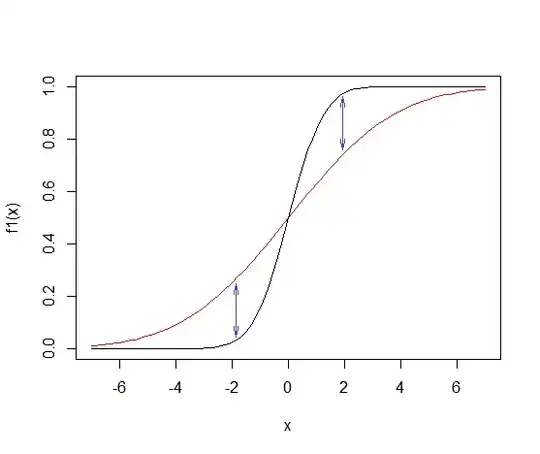
If we just plug this into the previous expression for the marginal density, we get:
$$\delta_{-}(y) = \rho \delta_{N(\mu_0,1)}(y) + (1-\rho) \delta_{\aleph}(y)$$
which looks like this
This is by all accounts a proper marginal: if I had thought of it, I could happily use it as a likelihood for my data without any need for negative probabilities by directly applying this distribution.
Question: Are there examples of negative densities being used in the context of latent variable models as a modeling device in order to define a generative model of observed data?
Such a thing exists in the context of the outcome of quantum phenomena, such as the double slit experiment. See this Wikipedia article for more on negative probabilities.