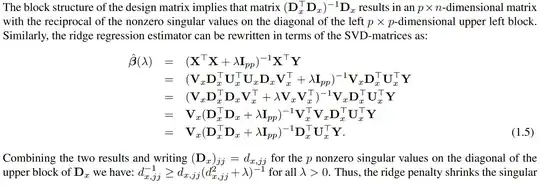0

I am trying to understand the following analysis of ridge regression.

enter image description here enter image description here enter image description here

I am new to SVD but I think I have a sufficient grasp on most of the content. There are two things I am struggling with.

  1. The last sentence. The ridge penalty shrinks which singular values? The singular values of $\mathbf X$, i.e. the eigenvalues of $\mathbf X^\top \mathbf X$, are what they are---they aren't being changed. It is however fairly simple to see that if the eigenvalues of $\mathbf X^\top \mathbf X$ are $d_{11}, \dots, d_{pp}$, then the eigenvalues of $\mathbf X^\top \mathbf X + \lambda \mathbf I$ are $d_{11} + \lambda, \dots, d_{pp} + \lambda$. Therefore the eigenvalues of $(\mathbf X^\top \mathbf X + \lambda \mathbf I)^{-1}$ are smaller than those of $(\mathbf X^\top \mathbf X)^{-1}$. Is that the point?

  2. I don't even understand the point of doing all the SVD stuff in order to show that $(\mathbf X^\top \mathbf X + \lambda \mathbf I)^{-1}$ has smaller eigenvalues than $(\mathbf X^\top \mathbf X)^{-1}$. I can do it easily without matrix decompositions. The only advantage I see to the SVD approach is that it gives insight into the limiting behavior of the ridge estimator as $\lambda$ becomes large (which is the next thing discussed after my screenshots).

I appreciate any help.

Rodrigo de Azevedo
  • 868
  • 7
  • 17
Novice
  • 531
  • 2
  • 9
  • 1
    "The eigenvalues of $(\mathbf X^\top \mathbf X + \lambda \mathbf I)^{-1}$ are smaller than those of $(\mathbf X^\top \mathbf X)^{-1}$. Is that the point?" Yes. https://stats.stackexchange.com/questions/220243/the-proof-of-shrinking-coefficients-using-ridge-regression-through-spectral-dec – Sycorax Nov 09 '21 at 19:05

0 Answers0