What is it called when an experimenter discards results that are too unexpected?

Question

There is a type of scientific error where an experimenter gets a result significantly different from prior researchers, assumes they made a mistake, and redoes the experiment until they get a more expected value, which they publish. I vaguely remember hearing about this in a Feynman book or video, where he described how correcting the known value of constants took longer than it should have because of this effect.

What is this effect called, and what are some famous examples?

UPDATE

I reworded the question to clarify what I meant by an "unexpected" result. Helpful commenters identified the Feynman anecdote:

• Is Feynman's claim about the history of measurements of the charge of the electron after Millikan accurate?
• Timeline of measurements of the electron's charge

The other posts don't include a term for the error.

Answer 1

Another answer has mentioned publication bias. However, that is not really what you were asking about, which is data dredging. A pertinent XKCD illustration is:

Answer 2

One way of framing this is as publication bias, which occurs when the outcome of an experiment influences the decision of whether or not to publish the result. This is a well-known form of bias that infects academic research. I'm not familiar with any "famous" examples, but there are a few works in the medical field that decribe some non-famous examples in Wilmherst (2007).

Examples of publication bias is inherently difficult to detect, since the non-published parts of the example are non-published (and therefore difficult to detect). Generally speaking, publication bias is detected through statistical analysis of reported metrics in published works. Consequently, most of the known "examples" of publication bias in academic literature are inferences of publication bias coming solely from the published works.

Answer 3

Example: Based on a real experiment, names of people and the organization (along with inconsequential details) are omitted to protect the guilty.

In a study comparing two methods (1 and 2) of manufacture, $n=100$ items were tested until failure. (Larger observed values are better.) Summary statistics for results x1 and x2 of the samples were as below:

summary(x1); length(x1);  sd(x1)
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
 0.1099  2.8264  7.0881 10.0057 12.8520 46.9993 
[1] 100
[1] 10.35345

summary(x2); length(x2);  sd(x2)
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
 0.1196  3.2247  8.0975 11.1469 15.9245 56.6384 
[1] 100
[1] 10.54756

boxplot(x1, x2, col="skyblue2", horizontal=T, notch=T)

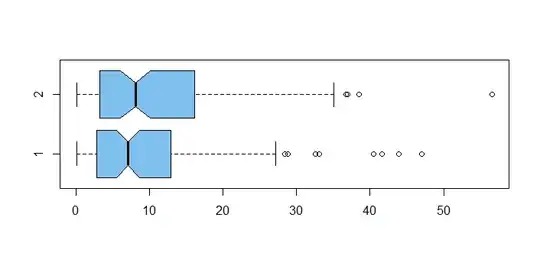
Everyone's favorite was Method 2 (even though more costly), and it had the larger mean. But the overlapping notches in the boxes suggest no significant difference. Also, a pooled 2-sample t.test, which "must be OK" because of the large sample sizes, finds no significant difference. [This was before Welch t tests became popular.] Experimenters were hoping for evidence that Method 2 was significantly better.

t.test(x1,x2, var.eq=T)

          Two Sample t-test

data:  x1 and x2
t = -0.77212, df = 198, p-value = 0.441
alternative hypothesis: 
 true difference in means is not equal to 0
95 percent confidence interval:
 -4.055797  1.773441
sample estimates:
mean of x mean of y 
 10.00571  11.14689 

The consensus was that the "outliers were messing up the t test" and should be removed. [No one seemed to notice that the new outliers had appeared with the removal of the original ones.]

min(boxplot.stats(x1)$out)
[1] 28.41372
y1 = x1[x1 < 28.4]
min(boxplot.stats(x2)$out)
[1] 36.73661
y2 = x2[x2 < 36.7]

boxplot(y1,y2, col="skyblue2", horizontal=T, notch=T)

Now with the "cleaned-up data" y1 and y2, we have a t test significant (just) below 5% level. Great joy, the favorite won out.

t.test(y1, y2, var.eq=T)

        Two Sample t-test

data:  y1 and y2
t = -1.9863, df = 186, p-value = 0.04847
alternative hypothesis: 
 true difference in means is not equal to 0
95 percent confidence interval:
  -4.37097702 -0.01493265
sample estimates:
mean of x mean of y 
 7.660631  9.853586 

To 'confirm they got it right', a one-sided ("because we already know which method is best") two-sample Wilcoxon test finds a significant difference (at very nearly the 5% level, but "nonparametric test are not as powerful"):

wilcox.test(y1, y2, alt="less")$p.val
[1] 0.05310917

Some years later when an economic crunch forced switching to cheaper Method 1, it became obvious that there was no practical difference between methods. In keeping with that revelation, I sampled the data for the current example in R as below:

set.seed(2021)
x1 = rexp(100, .1)
x2 = rexp(100, .1)

Note: You can Google and find an exact F-test to compare exponential samples, and it finds no difference, but nobody thought to use it at the time.