The problem with comparing simulated distributions as you describe is that the $n$ is arbitrary. In other words, you are only using simulation as a way of calculating the distribution function. So $n$ can be set to 100, 1,000, or 10,000; and the power to reject the null hypothesis becomes arbitrarily high. Conversely, fixing $n$ to some arbitrary value is of no use. From a testing perspective, a distribution is a population level summary whereas a random sample is a sample level summary, and so it doesn't make sense to perform statistical inference on populations when there is no "super"population to generalize to.
Having said that, you should crank up the simulation iterations as high as your CPU can handle to get the most precise estimate of the distribution functions as possible. Then "finding a difference" boils down to no more than actually finding some difference in the curve(s) and your job is done.
The matter of what comprises a "difference" is interesting. The supremum norm is not an intuitive comparison in practice. The KS test has interesting operating characteristics: it's a distribution-free test of the strong null hypothesis $F_1 = F_2$ where $F_1$ and $F_2$ are the distribution functions of the respective populations. You would, of course, reject the null if, for any $x$ at all $F_1(x) \ne F_2(x)$. However, you can easily calculate $\int ||F_1(x) - F_2(x)||^2 dx$ and call this the mean squared error. You can then rank or demonstrate how significant these differences are using a heatmap, by plotting higher intensities of color for relatively larger pairwise differences. This will show you which distributions are more disparate than the others.
set.seed(123)
BIGNUM <- 1e2
p <- 50
b <- rnorm(50, 0, 1)
x <- sapply(b, rnorm, n=BIGNUM, sd=1)
d <- apply(x, 2, ecdf)
pairs <- combn(1:p, 2)
delta <- apply(pairs, 2, function(ind) {
integrate(function(x)(d[[ind[1]]](x) - d[[ind[2]]](x))^2, lower=-Inf, upper=Inf, subdivisions=10000)$value
})
plot(t(pairs), pch=22, bg=rgb(1-delta/max(delta),1-delta/max(delta), delta/max(delta)))
ind <- pairs[, which.max(delta)]
plot(d[[ind[1]]], xlim=c(-7, 7))
lines(d[[ind[2]]])
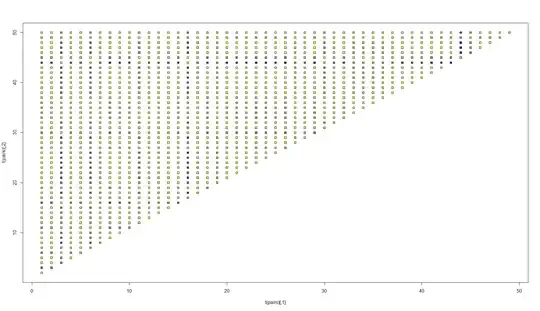
Note this image lets you pick out pairs 44 and 18 which, together, have the most discordant means in this simple normal example, (-1.97 and 2.17).
 Null Hypothesis - distribution belong to same population and they are different only by chance (randomness).
Null Hypothesis - distribution belong to same population and they are different only by chance (randomness).