1

There is going to be a lottery with a certain number of participants. The organizer is going to take a normal distribution with some parameters for the mean and variance. He will then generate some number of samples (say 5) and give them to the first participant, repeat for the second one and so on. The participants have to guess the variance. Whoever comes the closest (absolute difference between the estimated and actual values) will win. What should I do to maximize my chances of winning? We know there are two estimators for the variance of the normal distribution, $s^2$ which is unbiased and $\hat{\sigma}^2$ which is biased, but does better on the mean squared error criterion (see here). Is it better for this contest to use $\hat{\sigma}^2$ due to this?

Follow-ups: If we replaced a normal distribution with another and the variance by some other arbitrary parameter, is it always the case that the estimator with the smallest mean squared error should be used? Is it ever possible for two estimators to have the same mean squared error and for some other criterion to become the deciding factor in that case?

I realize I've asked a couple of questions here. The first one pertaining to the game where participants estimate the variance of the normal distribution is the most important.

ryu576
  • 2,220
  • 1
  • 16
  • 25
  • It is unlikely that an optimum strategy would involve a least-squares estimator of the variance. The strategy needs to be a statistic that has the highest possible chance of being closer to the true variance than the other participants will achieve: this loss function is qualitatively different than a least-squares loss. It would be helpful if you could focus your post on one specific question: currently it poses four questions. Which one is of greatest importance to you? – whuber Oct 24 '21 at 18:32
  • The first question is most important. Others are follow-ups. I can edit to clarify this. – ryu576 Oct 24 '21 at 18:51
  • But if the organizer said they would take the square difference between the participants guess and true value and reward the participant with the lowest square error, wouldn't the game stay effectively the same? – ryu576 Oct 24 '21 at 18:54
  • Yes, the game would remain the same--but the loss function nevertheless is not least-square loss. The loss is the *chance* of losing to any other participant. I suspect the optimal solution will exhibit a strong negative bias and will not be any standard or well-known estimator of the variance or the SD. – whuber Oct 24 '21 at 19:03
  • 1
    This question is about game theory. It is not asking what is the best estimator but instead, what is the estimator that has the biggest chance of winning from other estimators. (Possibly choosing a less good estimate might give you better chances because others are already choosing the good ones). – Sextus Empiricus Oct 24 '21 at 19:04
  • @SextusEmpiricus - I can define "best" anyway I want. In this case, I'm defining it as "highest chance of winning this game". Also, one can assume everyone else is very intelligent and won't just go with unbiased or least square estimators blindly if that isn't the best thing to do. – ryu576 Oct 24 '21 at 19:05
  • 1
    @ryu576 the problem is that the matter becomes not just a question about making the best guess, but also analysing what the others will do. – Sextus Empiricus Oct 24 '21 at 19:40
  • @SextusEmpiricus - maybe you're right, but that isn't obvious to me. I have a suspicion that the best strategy will be to ignore what others are doing and just do the best you can do. – ryu576 Oct 24 '21 at 19:55
  • BTW, if someone does sponsor such a game (maybe I will when I'm rich), it'll be a shame if people who are competent at statistics end up with no advantage. – ryu576 Oct 24 '21 at 19:57

1 Answers1

3

We know there are two estimators for the variance of the normal distribution, $s^2$ which is unbiased and $\hat{\sigma}^2$ which is biased, but does better on the mean squared error criterion (see here). Is it better for this contest to use $\hat{\sigma}^2$ due to this?

No,

Or at least, optimizing squared error (or absolute error since it is about the smallest absolute error who wins), is not a uniform best winning strategy (it does not win from all other strategies).

Bias with shrinking and biased estimators with lower mean error

Say, we use only the standard error computed as

$$s^2 = \frac{1}{n-1} \sum{(x_i-\bar{x})^2}$$

It is the sufficient statistic and other data are not more helpful. (in the simulations below we simulate this by drawing from a chi-squared distribution)

We can use estimators with a particular scaling.

$$\hat\sigma^2_f = f s^2$$

If $f=1$ then we have the unbiased estimator. But as we see in the figure below, it is a lower value of $f$ that performs better (has a lower error in terms of mean squared error or mean absolute error).

The figure below is computed for sample size $n = 5$.

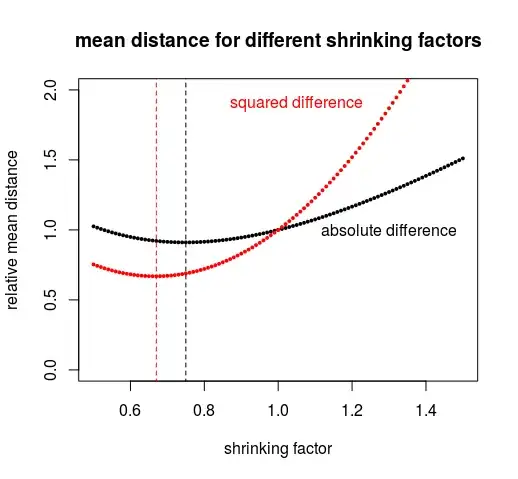
shrinking/bias reduces mean error

See also here for a demonstration of this shrinking factor: Bias / variance tradeoff math

Lowest mean error is not necessarily the best strategy

It is not about making the smallest possible mean error.

Instead, it is about making often a smaller error (that's what makes you win from opponents). It is better to have very small errors combined with very large errors, than only medium errors. Even when the latter is on average better.

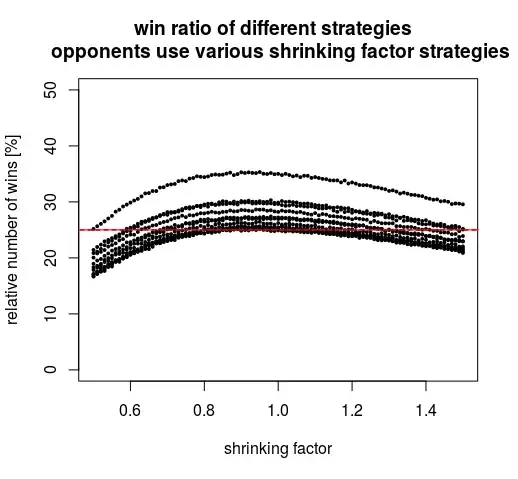
Below we see the performance of alternative strategies, in the situation that all your opponents use the strategy that aims for the lowest mean error.

If we use the same strategy as the opponents (the vertical lines), then we all have the same strategy and have all equal chances to win (the figure is for 3 opponents, 4 contestants in total so 25% win percentage).

We see that using less shrinking, will improve the win percentage. With less shrinking the mean error is bigger, but this is countered by being more often very close (we do not care if for some percentage we make extremely large errors, optimizing those is not gonna make us win).

different wins for different strategies

The above graph is the situation when your three opponents use the lowest mean distance strategy (either based on lowest mean square distance or lowest mean absolute distance). But what if they would do something else? The graph below plots the situation but now instead of two curves we plot eleven curves where for each curve the opponents use a different shrinking factor (from 0.5 to 1.5 in steps from 0.1, giving 11 curves). You see that a shrinking factor a bit above 0.9 is giving the best result, no matter what the opponents do. In the worst case, the opponents choose the same strategy and you all have an equal probability to win.

with many different opponent strategies giving 11 curves

Wrap up

The above is simulations. They show at least that minimizing the mean squared error is not necessarily the best strategy.

But, in order to compute which strategy is best, you would need to perform more simulations. Ideally one would be able to write formulas (it would be something with order distributions) such that no computations are necessary.

If there is an optimal strategy then it probably aims to optimize a small percentage of the guesses (a fraction a bit above 1/n where n is the number of opponents) to be with a very small distance. We do not care if in the rest we make huge errors.

With some testing for other numbers of opponents, it seems that the more opponents you have, the more the optimal strategy shifts towards the unbiased estimate with $f=1$.

  • With few opponents it is better to optimize the mean error and use a biased estimate.
  • With many opponents it is better to minimize the bias (which increases the frequency of small errors, at the cost of some very large errors).

computer code for simulations and graphs

### init
set.seed(1)               # set random seed for reproducibility
m = 10^5                  # number of samples to compute statistics
nu = 4
x = rchisq(m,nu)          # draw sample from chi-squared distribution
                          # this is the sum of squares that you get 
                          # from nu+1 normal distributed samples

fs = seq(0.5,1.5,0.01)    # parameter of shrinking factors that we are gonna test

sy = sum(abs(x-4))        # compute absolute deviation error of non biased estimator
sy2 = sum(abs(x-4)^2)     # compure squared error of non biased estimator


### function to compute absolute deviation error
### of biased estimator (shrinking with a factor fi)
reld = function(fi) {
  sum(abs(fi*x-4))/sy
}
reld = Vectorize(reld)

### function to compute squared deviation error
### of biased estimator (shrinking with a factor fi)
reld2 = function(fi) {
  sum(abs(fi*x-4)^2)/sy2
}
reld2 = Vectorize(reld2)

### plot error comparison of biased estimators with unbiased estimator
plot(-10,-10, xlim = c(0.5,1.5), ylim = c(0,2),
     ylab = "relative mean distance", xlab = "shrinking factor",
     main = "mean distance for different shrinking factors")
y1 = reld(fs)
y2 = reld2(fs) 
points(fs, y1, pch = 21, col = 1, bg = 1, cex = 0.4)
points(fs, y2, pch = 21, col = 2, bg = 2, cex = 0.4)

text(1.3,1, "absolute difference")
text(1.05,1.9, "squared difference", col =2)


### lines of the optimum
x1 = fs[which.min(y1)]
lines(x1*c(1,1), c(-1,3), lty = 2)
x2 = fs[which.min(y2)]
lines(x2*c(1,1), c(-1,3), col = 2, lty = 2)

### function to get the best result (distance) from n oponents
sim = function(fi,n) {
  x = matrix(rchisq(m*n,nu),m)       ### measurements of your opponents
  d = abs(fi*x-nu)                      ### score of opponents if they would use bias fi
  y = apply(d, 1, function(x) min(x))  ### the score of your best opponent
  y
}

### function to get the best result (distance) from n oponents
### same as above but for squared distance
sim2 = function(fi,n) {
  x = matrix(rchisq(m*n,nu),m)
  d = abs(fi*x-nu)^2
  y = apply(d, 1, function(x) min(x))  
  y
}

opp = 3
score1 = sim(x1,opp)
score2 = sim2(x2,opp)

### function to test strategy against ensemble
getwins = function(fi) {
  y = sim(fi,1)     
  wins = sum(y<score1)  ### count wins
  wins/m           ### compute proportion
}
getwins = Vectorize(getwins)

### function to test strategy against ensemble
getwins2 = function(fi) {
  y = sim2(fi,1)     
  wins = sum(y<score2)  ### count wins
  wins/m           ### compute proportion
}
getwins2 = Vectorize(getwins2)



### plot win comparison of different strategies
wins = getwins(fs)
wins2 = getwins2(fs)

plot(-10,-10, xlim = c(0.5,1.5), ylim = c(0,2)*100/(opp+1),
     ylab = "relative number of wins [%]", xlab = "shrinking factor",
     main = "win ratio of different strategies  \n opponents use lowest mean distance strategy")

points(fs,100*wins, pch = 21, col = 1, bg = 1, cex = 0.4)
points(fs,100*wins2, pch = 21, col = 2, bg = 2, cex = 0.4)

lines(c(0,2),c(1,1)*100/(opp+1), lty = 2)
lines(x1*c(1,1), c(-100,300))
lines(x2*c(1,1), c(-100,300), col = 2)

text(1.3,20, "absolute difference")
text(1.2,30, "squared difference", col =2)
Sextus Empiricus
  • 43,080
  • 1
  • 72
  • 161
  • 1
    Note, while reviewing the code I realize that in order to win the game it does not matter whether we compare squared distance or absolute distance. If you have the lowest for one, then you have it also for the other. So this simplifies the computations and one does not need to write the functions two times for the two squared/absolute cases. This will also make any potential analytical approach easier. Instead of optimizing the absolute error (which is difficult), one can work with optimizing the distribution for the squared distance (whose distribution is some shifted gamma distribution). – Sextus Empiricus Oct 24 '21 at 23:42
  • +1 This is the right way to think about the question. But you can do better than simulations: just compute the integrals. That should work well for small numbers of players. It would be interesting to find a demonstration of a Nash equilibrium--I haven't even been able to prove that yet. One thing I suspect is that as the number of players increases, the optimum strategy is to estimate the *mode* and adjust that estimate to agree with the mean. This must come close to maximizing the chance of being closest to the mean. – whuber Oct 25 '21 at 13:36
  • @whuber a game theoretic element isn't strong in this example. It's just best to be as good as possible. However, when with a Bayesian approach, or when participants have partly the same data, then there will be the effect that competitors are likely close to your own guess, because they share the same data or prior. In that case it might be an option to choose a less good strategy not because it is better, but because less competitors will do the same and so you are less likely to be close to the answer, but if you are close to the answer then it is less likely that others are close as well. – Sextus Empiricus Oct 25 '21 at 13:45
  • @whuber I used simulations (to show the principle and get an idea) because describing the distribution, necessary to do the integrals, is not very typical. For instance, when I describe the distribution of the distance of the estimate than I get some sort of folded distribution. Say the estimate is distributed as $X \sim \chi^2(\nu = 4)$ and we estimate the mean which is equal to $\nu = 4$. Then the CDF for a distance $D$ is $$P(d \leq D) = P(\nu -d \leq X \leq \nu + d)$$ and the pdf contains two terms $$f_D(d) = f_X(\nu -d) + f_X(\nu + d)$$ – Sextus Empiricus Oct 25 '21 at 13:53
  • In addition, the integration becomes complex with many competitors. One would be more efficient when expressing some order distribution but since the pdf and cdf are not typical it is difficult to find a simple expression for the distribution of the best result from the competitors. (and then when the simulations showed that for many competitors it is anyway the best strategy to be as close to the unbiased sample anyway*, I lost interest). *more precise it is not about bias but about choosing the strategy with the highest probability density for being close to the true answer. – Sextus Empiricus Oct 25 '21 at 13:57
  • That last phrase in your latest comment captures the essence of the problem. – whuber Oct 25 '21 at 14:00
  • Yes that last phrase is also like your *" One thing I suspect is that as the number of players increases, the optimum strategy is to estimate the mode and adjust that estimate to agree with the mean. This must come close to maximizing the chance of being closest to the mean. "* In this problem this happens to be when we use no scaling/shrinking... – Sextus Empiricus Oct 25 '21 at 14:00
  • An interesting detail is that I looked only at shrinking. So the distribution with the highest density for the correct answer is with zero shrinking. **But that is not the mode!** The mode of a chi-squared distribution is smaller than the mean. Instead of using shrinking we could also 'shift' the answer (normally not a strategy to improve mean error because it does not decrease variance). The problem is, how do we know by how much we need to shift? With shrinking it is dimensionless and everything is independent from the value of the true $\sigma^2$. But with a shift this is not the case. – Sextus Empiricus Oct 25 '21 at 14:05
  • Yes, I pondered those things, too. I concluded that the shift cannot work because for some parameter values it will be obviously inferior to standard estimates. I also contemplated expansion, not just shrinking, specifically because it moves the mode towards the mean. Unfortunately, it also greatly increases the variance. I think some worked examples--using high-precision numerical integration, not simulation--will be revealing. The integration is not as bad as you make it sound, at least for two players: it's just a univariate integral. – whuber Oct 25 '21 at 14:09
  • 1
    https://i.stack.imgur.com/1SLqh.png a problem with expansion is that it does shift the mode, but at the same time lower it. It seems like a shrinking/expansion of 1 is the best. (I am sure that this can be computed exactly, but when the simulations shows that it is so close to 1, then I intuitively believe it is fine) – Sextus Empiricus Oct 25 '21 at 14:18