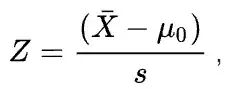1

How would one calculate the p-value from a doubly robust model enter image description here

I could used the boot.pval r package and set the theta_null (The value of the parameter under the null hypothesis) 0, using student t-test as method.

Alternatively, I could use the approach below referencing: Computing p-value using bootstrap with R

How could one obtain the p-value for the doubly robust model? If by not by the approach below, then how?

time = c(14,18,11,13,18,17,21,9,16,17,14,15,
     12,12,14,13,6,18,14,16,10,7,15,10)
group=c(rep(0:1, each=12))
sleep = data.frame(time, group)

require(boot)
diff = function(d1,i){
    d = d1[i,]
    Mean= tapply(X=d$time, INDEX=d$group, mean)
    Diff = Mean[1]-Mean[2]
    Diff
}

set.seed(1234)
b3 = boot(data = sleep, statistic = diff, R = 5000, strata=sleep$group)

b3.under.H0 <- b3$t - mean(b3$t)

pvalue = mean(abs(b3.under.H0) > abs(b3$t0))

pvalue

Updated: 2021-10-26:

My bootstrap distribution looks suitable for normal distribution but not t-distribution. When I used the percentile p-value calculation, the value 0.007 looked sensible. boot.pval does not seem to be giving sensible results p=1x10-16, nor does normal p-value.

enter image description here

Updated: 2021-10-26 17:09:

For Null hypothesis H0: μ=μ0 vs alternative hypothesis H1: μ≠μ0 , it is two-tailed.

enter image description here

which two-tailed p-values can be calculated as 2Φ(−|Z|) (for two-tailed tests) where Φ is the standard normal cumulative distribution function.

SysEng
  • 73
  • 9
  • 1
    One way would be to bootstrap the standard error (i.e., as the standard deviation of the bootstrap distribution of estimated effects) and then use a Z-test. – Noah Oct 22 '21 at 15:37
  • Are you able to give an example of how to use the Z-test to derive p-value? Is that suitable for the distribution I have? I would like to verify my results, but I do not really trust the boot.pval function. See my updated question @Noah. – SysEng Oct 26 '21 at 09:40
  • 1
    A Z-test involves dividing the estimate by its standard error and converting the resulting z-statistic into a p-value. The standard error estimate is the standard deviation of the bootstrap distribution. You can also use the analytical formulas for computing the standard error. – Noah Oct 26 '21 at 14:52
  • 1
    I don't understand what your update means. Nothing about your plot really indicates whether a Z or T distribution is appropriate. How do you know .007 is sensible and 1xe-16 is not sensible? The DR estimator is asymptotically normal so a Z-test would be the usual test. Otherwise just compute confidence intervals and move on. A p-value doesn't give you that much more information. – Noah Oct 26 '21 at 14:55
  • please see my updated question to see if it is correct now? I guess the Null hypothesis is 1 when we are considering the odds ratio for DR. But I do not understand why wikipedia suggests 2Φ(−|Z|) whereas you suggested to divide by sd again Z / SD, is there a reference you could provide ? @Noah, thanks. – SysEng Oct 26 '21 at 16:05
  • I have resolved this, the p-value for normal z-test concords with percentile p-value of non-significance. Thanks for the help @Noah (+2). https://cran.r-project.org/web/packages/distributions3/vignettes/one-sample-z-test.html here is a nice link for doing the calculation with z-test – SysEng Oct 26 '21 at 16:44

0 Answers0