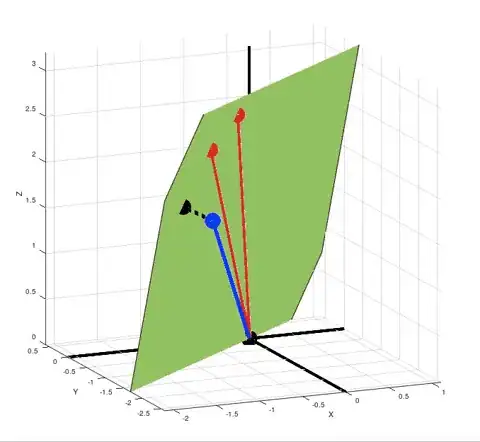
Multicollinearity in OLS linear regression can be a cause of high sensitivity of the model to small changes in the dataset. It can be visually shown for 3 dimensions:
Column space of feature matrix can just turn around in response to small change in one of the feature vectors. So the new plane will drastically diverge from the old one, which results in new projection of target vector and therefore new coefficients.
But it's apparent only for 3 dimensions. Is there a way to prove (or somehow show) that the coefficient estimates may change erratically in response to small changes in the data for higher dimensions as well?
I've already seen all the related answers on this site and wasn't able to find anything satisfactory except this one, but it talks about 3 dimensions. Also this answer didn't seem to primarily answer my question.